|
Блиц-курс – Кратные и криволинейные интегралы |
2.6.2. Центр тяжести телаПодобно тому, как задача о вычислении центра тяжести плоской фигуры решалась с помощью двойного интеграла, задача об отыскании центра тяжести тела решается аналогичным способом – с помощью тройного интеграла. Что такое центр тяжести тела, довольно удачно объяснил ещё Архимед. Если тело подвесить на нить за центр тяжести, то оно будет сохранять равновесие в любом положении (как бы мы его предварительно ни повернули). В известной степени это не реализуемо (таки центр тяжести внутри тела), но зато очень понятно. И вполне в стиле древнегреческого учёного, который просил дать ему точку опоры, чтобы с помощью рычага перевернуть Землю. Центр тяжести Если же тело однородно (стеклянное, оловянное, пластмассовое и т.д.), то формулы упрощаются. Так как плотность Для центра тяжести однородного тела справедливы следующие утверждения: – если у тела есть центр симметрии, то он является центром тяжести (простейший пример – центр шара); – если у тела существует линия симметрии, то центр тяжести обязательно принадлежит данной линии; – если у тела есть плоскость симметрии, то центр тяжести непременно лежит в этой плоскости. Как видите, практически полная аналогия с центром тяжести плоской фигуры. Ну и, само собой, не могу не порадовать вас тематической задачей: Пример 42 Найти центр тяжести однородного тела, ограниченного поверхностями Решение: искомое тело ограничено координатными плоскостями и плоскостью
Координаты 1) Сначала вычислим объём тела. Его, кстати, можно узнать заранее, пользуясь известной задачей геометрии об объёме
тетраэдра. Объём тетраэдра равен 1/6-й объёма прямоугольного параллелепипеда, построенного на его трёх смежных рёбрах. В нашем
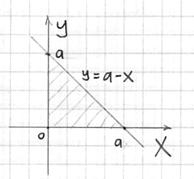
случае параллелепипед представляет собой куб с ребром «а», а посему: В примерах с громоздкими преобразованиями рекомендую записывать решение «столбиком» – меньше шансов запутаться: 2) Вычислим «иксовый» интеграл, …и местечка у меня тут не хватает, поэтому решение в столбик отменяется: Учитывая симметрию тела, две другие координаты должны получиться такими же. Теперь ошибочный финал практически исключён! И
я вам предлагаю рассчитать …А вы, наверное, не так давно и представить себе не могли, что окажетесь в эпицентре такого кошмара =)
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за пару дней!
Научись решать за пару дней!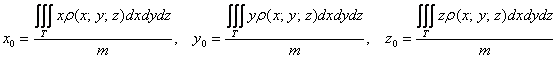 , где
, где 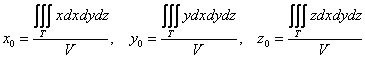 , а объём тела рассчитывается (ещё не забыли? =))
, а объём тела рассчитывается (ещё не забыли? =)) 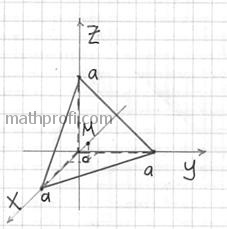
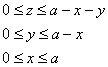
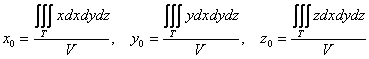 , где
, где 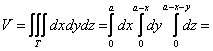
 (да, так можно – сразу снести
(да, так можно – сразу снести

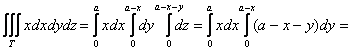
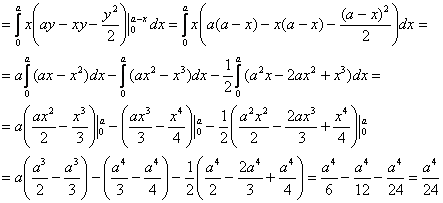
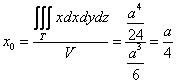 , ну что же, выглядит правдоподобно, по крайне мере, мы «попали внутрь» тела.
, ну что же, выглядит правдоподобно, по крайне мере, мы «попали внутрь» тела. 3. Криволинейные интегралы
3. Криволинейные интегралы 2.6. Физические приложения тройного интеграла
2.6. Физические приложения тройного интеграла