|
Блиц-курс – Кратные и криволинейные интегралы |
2.6. Физические приложения тройного интегралаСначала разомнёмся физически (давно пора), тело – в дело :). Пожалуйста, встаньте и найдите какой-нибудь пакет или мешок. Можно коробку. Теперь походите по квартире, ну или по улице и наведём порядок. А именно, наполним тару мусором. …Очень хорошо, молодцы! В результате ваших трудов получено ограниченное тело неоднородной плотности. Как говорится, есть бумажка, а есть жестяная крышка. Воздух, кстати, тоже обладает вполне определённой плотностью. Напоминаю, что физическая плотность – есть отношение единицы массы к единице объёма, например, 100 грамм на кубический метр (средняя плотность хлопка) или 19,32 грамма на кубический сантиметр (да, всего лишь на сантиметр – это плотность чистого золота). Ставим мешок рядышком и читаем дальше: 2.6.1. Масса телаРассмотрим неоднородное (переменной плотности) тело Но на практике не всё так легко: Пример 50 Вычислить массу неоднородного тела, ограниченного поверхностями Решение: искомое тело ограничено цилиндром Порядок обхода тела очевиден: Осталось преобразовать подынтегральную функцию: Вычисления элементарны: Ответ: Пример 51 Вычислить массу неоднородного тела, ограниченного поверхностями Краткое решение в конце книги. И старая песня о главном:
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за пару дней!
Научись решать за пару дней!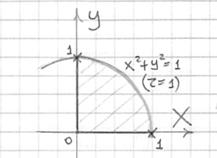
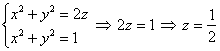 и выполним пространственный чертёж:
и выполним пространственный чертёж: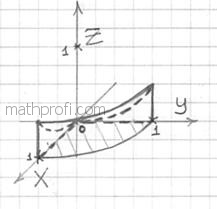
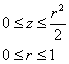
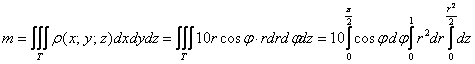

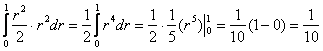
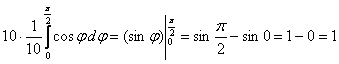
 2.6.2. Центр тяжести тела
2.6.2. Центр тяжести тела 2.5. Тройной интеграл в сферических координатах
2.5. Тройной интеграл в сферических координатах