2.4. Как вычислить произвольный тройной интеграл?
Отработаем технику и тонкости лечения пациентов 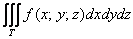 , у которых подынтегральная функция трёх
переменных , у которых подынтегральная функция трёх
переменных 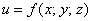 в общем
случае отлична от константы и непрерывна в области в общем
случае отлична от константы и непрерывна в области 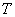 : :
Пример 42
Вычислить 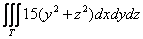 по области по области 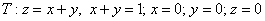
На практике тело также обозначают буквой 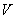 , но это всё-таки не очень хороший вариант, ввиду того, она
«зарезервирована» под обозначение объёма. , но это всё-таки не очень хороший вариант, ввиду того, она
«зарезервирована» под обозначение объёма.
И вновь скажу, чего делать НЕ НАДО. По аналогии с двойными интегралами, здесь не
нужно пользоваться свойством линейности и представлять интеграл в виде 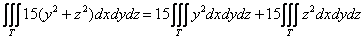 . Хотя, если очень хочется, то можно. В конце концов, есть и
небольшой плюс – запись будет пусть длинной, но зато менее загромождённой. Но такой подход всё-таки не стандартен. . Хотя, если очень хочется, то можно. В конце концов, есть и
небольшой плюс – запись будет пусть длинной, но зато менее загромождённой. Но такой подход всё-таки не стандартен.
В самом алгоритме решения новизны будет немного. Сначала нужно разобраться с областью интегрирования и её «тенью». Проекция тела на плоскость 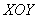 представляет собой до боли знакомый треугольник: представляет собой до боли знакомый треугольник:
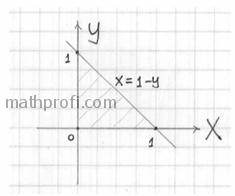 Сверху тело ограничено плоскостью Сверху тело ограничено плоскостью 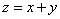 , которая проходит
через начало координат. Предварительно, к слову, нужно обязательно проверить (мысленно либо на
черновике), не «срезает» ли эта плоскость часть треугольника. Для этого находим её линию пересечения с координатной
плоскостью , которая проходит
через начало координат. Предварительно, к слову, нужно обязательно проверить (мысленно либо на
черновике), не «срезает» ли эта плоскость часть треугольника. Для этого находим её линию пересечения с координатной
плоскостью 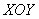 , т.е. решаем простейшую
систему: , т.е. решаем простейшую
систему: 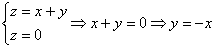 – нет, данная прямая (на
чертеже отсутствует) проходит «мимо» заштрихованной области, и проекция тела на плоскость – нет, данная прямая (на
чертеже отсутствует) проходит «мимо» заштрихованной области, и проекция тела на плоскость  действительно представляет собой весь треугольник. действительно представляет собой весь треугольник.
Не сложен здесь и пространственный чертёж:
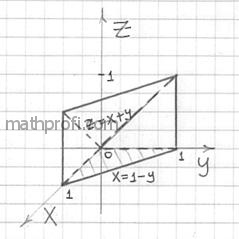
В действительности можно было ограничиться только им, поскольку проекция очень простая. …Ну, или только чертежом проекции,
так как тело тоже простое =) Однако совсем ничего не чертить, напоминаю – это плохой
выбор.
Выберем следующий порядок обхода тела:
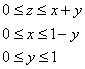
и перейдём к повторным интегралам:
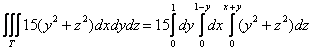
Актуализируем элементарное правило:
Когда функция 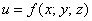 дифференцируется по какой-либо переменной, то два
других аргумента считаются константами. дифференцируется по какой-либо переменной, то два
других аргумента считаются константами.
И коль скоро так, то очевидно, справедливо и обратное:
Когда функция 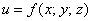 интегрируется по какой-либо переменной, то два других аргумента считаются
константами. интегрируется по какой-либо переменной, то два других аргумента считаются
константами.
С повторными интегралами разберёмся друг за дружкой; ввиду кропотливости вычислений, я закомментирую почти каждый
шаг:
1) Вычислим внутренний интеграл, сначала решение, затем комменты:
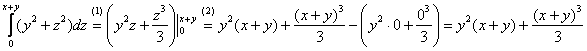
(1) При интегрировании по «зет» 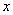 и и
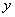 считаются константами. В данном случае
присутствует только «игрек», но это не меняет дела. Мысленно либо на черновике выполняем проверку, а именно
берём частную производную по «зет»: считаются константами. В данном случае
присутствует только «игрек», но это не меняет дела. Мысленно либо на черновике выполняем проверку, а именно
берём частную производную по «зет»:
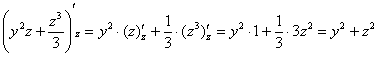 , что и хотелось увидеть. , что и хотелось увидеть.
(2) Теперь используем формулу Ньютона-Лейбница: сначала ВМЕСТО «зет» подставляем верхний предел интегрирования 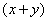 , затем – нижний предел (ноль). После
подстановок буквы «зет» остаться не должно! , затем – нижний предел (ноль). После
подстановок буквы «зет» остаться не должно!
Сносим трофей в следующий интеграл:
2) По существу, решение свелось к двум переменным и к двойному интегралу:
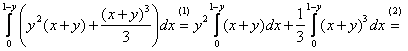
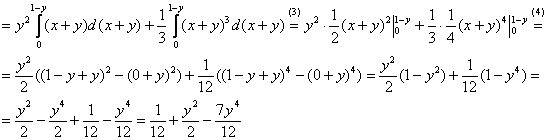
(1) Используем свойства линейности интеграла, принимая во внимание тот факт, что «игрек» считается константой. Не
возбраняется оставить интеграл единым, раскрыть скобки и привести подобные слагаемые, но это менее рационально (можете
попробовать).
(2) Используем метод подведения под знак дифференциала. Если рассуждения воспринимаются совсем тяжко, мысленно
замените «игрек» каким-нибудь конкретным числом, например, «пятёркой».
(3) Интегрируем по «икс» и выполняем проверку дифференцированием:
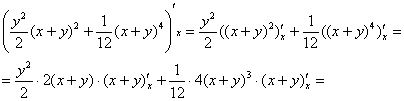
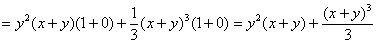 – исходная функция. – исходная функция.
(4) Используем формулу Ньютона-Лейбница. Сначала ВМЕСТО «икс» (переменной, по которой проводилось
интегрирование) подставляем 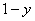 , затем –
ноль. После подстановок пределов интегрирования буквы «икс» остаться не должно! , затем –
ноль. После подстановок пределов интегрирования буквы «икс» остаться не должно!
Причёсываем результат и сносим его в последний интеграл, не забывая про находящуюся перед интегралом константу
(пятнадцать):
3) Не расслабляемся:
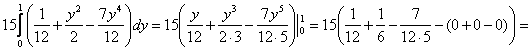
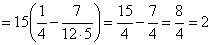
Ответ: 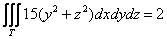
Результат безразмерен – просто число и всё. Но это «просто» лишь в рамках предложенной задачи, у тройного интеграла тоже есть физический смысл, о котором мы поговорим позже. Следующий пример для
самостоятельного решения:
Пример 43
Вычислить тройной интеграл
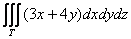 , , 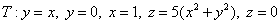
До сих пор мы рассматривали два способа решения – это проецирование на плоскость 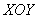 и выбор порядка обхода проекции. Но на самом деле комбинаций больше – тело
можно спроецировать на любую из трёх координатных плоскостей и каждую проекцию обойти двумя путями. Таким образом, получается
шесть способов решения. И логично предположить, что некоторые из них могут быть проще, а некоторые –
труднее. и выбор порядка обхода проекции. Но на самом деле комбинаций больше – тело
можно спроецировать на любую из трёх координатных плоскостей и каждую проекцию обойти двумя путями. Таким образом, получается
шесть способов решения. И логично предположить, что некоторые из них могут быть проще, а некоторые –
труднее.
Наверняка многие обратили внимание, что в Примере 42 я выбрал более редкий
порядок обхода проекции, хотя ничто не мешало пойти «обычным» путём. Это не случайность. В результате нахождения интеграла
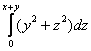 получена сумма получена сумма 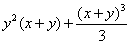 , в которой чуть выгоднее считать константой именно
«игрек», что при прочих равных условиях (из уравнения прямой , в которой чуть выгоднее считать константой именно
«игрек», что при прочих равных условиях (из уравнения прямой 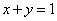 одинаково легко получить одинаково легко получить 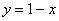 и и 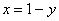 ) упрощает решение. А в некоторых задачах выбор порядка
интегрирования и вовсе становится ОЧЕНЬ важным: ) упрощает решение. А в некоторых задачах выбор порядка
интегрирования и вовсе становится ОЧЕНЬ важным:
Пример 44
Вычислить тройной интеграл 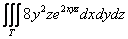 по
области по
области 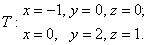
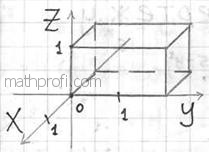 Решение:
область интегрирования ограничена шестью плоскостями и представляет собой прямоугольный параллелепипед: Решение:
область интегрирования ограничена шестью плоскостями и представляет собой прямоугольный параллелепипед:
У незамысловатых областей, как эта, можно не обращать внимания на проекции и придерживаться следующего
правила: обход тела осуществляется в направлениях координатных осей. Пределы интегрирования здесь
очевидны:
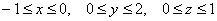
Но вот с порядком обхода не всё так просто. Если выбрать «традиционный» путь и сначала интегрировать по «зет», то
получается интеграл 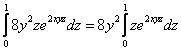 , который нужно
брать по частям. Аналогичная история, если в первую очередь интегрировать по «игрек»: , который нужно
брать по частям. Аналогичная история, если в первую очередь интегрировать по «игрек»:  – тут даже дважды по частям. – тут даже дважды по частям.
Наиболее выгодным путём является первоочередное интегрирование по «икс», в этом случае переменные 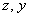 , а значит, и множитель , а значит, и множитель 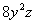 считаются константами: считаются константами:
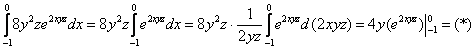
Перед тем, как подставлять пределы интегрирования, выполняем проверку:
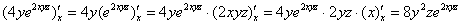 – получена исходная подынтегральная
функция. Продолжаем решение: – получена исходная подынтегральная
функция. Продолжаем решение:
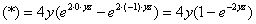
Буква «икс» (переменная интегрирования) испарилась, как оно и должно быть.
Осталось два направления обхода: 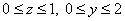 , и
следующий интеграл рациональнее взять по «зет» (чтобы множитель , и
следующий интеграл рациональнее взять по «зет» (чтобы множитель 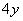 считался константой): считался константой):
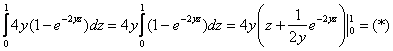
Промежуточная проверка:
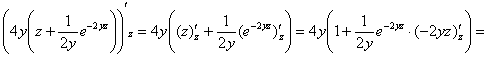
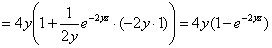 , едем дальше: , едем дальше:
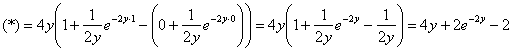
В качестве дополнительного контроля снова смотрим, исчезла ли после подстановок переменная, по которой интегрировали
(«зет»)? И, наконец, оставшееся направление обхода 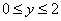 и оставшийся интеграл: и оставшийся интеграл:
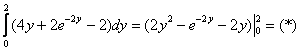
Контроль: 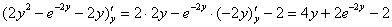
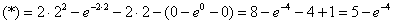 , готово. , готово.
При подстановках следует проявлять повышенное внимание, так, например, при подстановке нуля в выражение 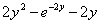 второе слагаемое можно машинально счесть за
ноль. второе слагаемое можно машинально счесть за
ноль.
На чистовике, конечно же, не нужно всё расписывать так подробно, анализ порядка интегрирования и промежуточные проверки
осуществляются мысленно либо на черновике. Решение оформляется стандартно в 3 пункта, но читатели с хорошим уровнем подготовки
могут записать его и «одной строкой»:

Ответ: 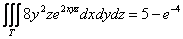
Наверное, это понятно, но на всякий случай закомментирую: буквенные множители-«константы» в интегралах следует перемещать
справа налево последовательно и без «перескоков» – до тех пор, пока каждая буква «не встретит свой интеграл».
Условный пример:
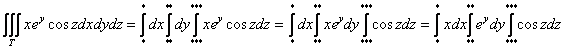
Но это если переменные можно вообще отделить, так, у условного интеграла:
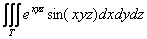 – ничего отделить и
переместить нельзя. – ничего отделить и
переместить нельзя.
Аналогичное задание для самостоятельного решения:
Пример 45
Вычислить тройной интеграл
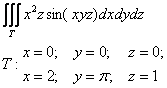
Примерный образец чистового оформления задачи в конце книги.
Точно так же, как и при нахождении объёма, в некоторых интегралах удобен переход к цилиндрической системе координат, и мы, конечно же, разберём парочку задач;
напоминаю, что все примеры я беру из реальных студенческих самостоятельных и контрольных работ. Поэтому не ленимся:
Пример 46
Вычислить тройной интеграл  по области,
ограниченной поверхностями по области,
ограниченной поверхностями 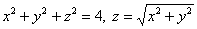 . .
Решение: уравнение 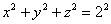 задаёт сферу с центром в начале координат радиуса 2, и осталось
прояснить ситуацию с уравнением задаёт сферу с центром в начале координат радиуса 2, и осталось
прояснить ситуацию с уравнением 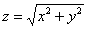 . Для этого
возведём обе его части в квадрат: . Для этого
возведём обе его части в квадрат: 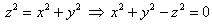 –
каноническое уравнение конической поверхности, при этом функция –
каноническое уравнение конической поверхности, при этом функция 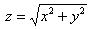 задаёт верхнюю её часть (поскольку задаёт верхнюю её часть (поскольку 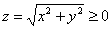 при любых «икс», «игрек»). при любых «икс», «игрек»).
Найдём линию пересечения сферы и конуса, для этого составим и решим систему, состоящую из их уравнений:
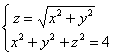 – подставим – подставим 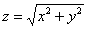 во 2-е уравнение: во 2-е уравнение:
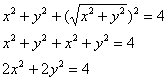
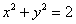 – подставим в 1-е уравнение системы: – подставим в 1-е уравнение системы:
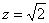
Таким образом, на высоте 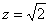 конус
пересекается со сферой по окружности конус
пересекается со сферой по окружности 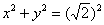 . Сверху область . Сверху область 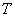 ограничена сферой, снизу – конусом, и в результате у нас
получается вот такое симпатичное эскимо: ограничена сферой, снизу – конусом, и в результате у нас
получается вот такое симпатичное эскимо:
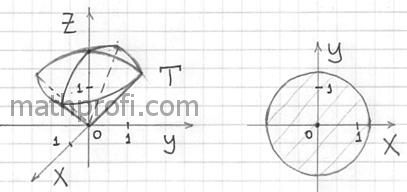
Проекцией тела на плоскость 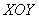 является круг является круг 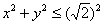 и это наталкивает на мысль перейти к
цилиндрическим координатам: и это наталкивает на мысль перейти к
цилиндрическим координатам: 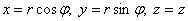 . В
этой системе координат уравнение окружности принимает вид . В
этой системе координат уравнение окружности принимает вид 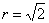 и, очевидно, порядок обхода проекции таков: и, очевидно, порядок обхода проекции таков: 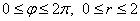 . Найдём уравнения поверхностей в новой системе координат: . Найдём уравнения поверхностей в новой системе координат:
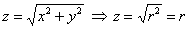 – уравнение верхней части конуса; – уравнение верхней части конуса;
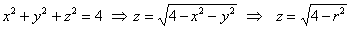 – уравнение верхней полусферы. – уравнение верхней полусферы.
«Луч лазера» входит в тело 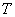 снизу через конус снизу через конус 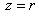 и выходит из него сверху через сферу и выходит из него сверху через сферу 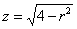 , следовательно, вертикальное направление обхода: , следовательно, вертикальное направление обхода: 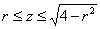 . .
В результате:
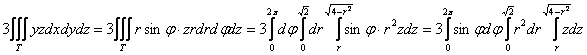
Здесь мы на первом шаге перешли к цилиндрической системе координат, учитывая, что 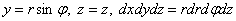 , на втором шаге расставили повторные интегралы в соответствии с
проведённым выше анализом, и на третьем – расставили множители по своим «родным» интегралам. , на втором шаге расставили повторные интегралы в соответствии с
проведённым выше анализом, и на третьем – расставили множители по своим «родным» интегралам.
Повторные интегралы щёлкаем друг за дружкой:
1) 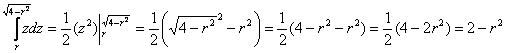
2) Результат предыдущего пункта подставляем в средний интеграл, не забывая, что там уже есть множитель
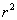 : :
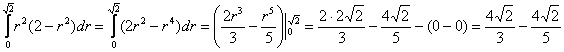
3) И, наконец, полученную константу подставляем во внешний интеграл, причём её можно сразу вынести. Не забываем о
множителе 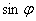 и тройке перед
интегралом: и тройке перед
интегралом:
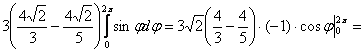
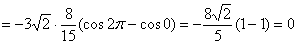 , готово. , готово.
Ответ: 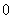
Примечание: при вычислении 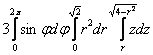 можно
было сразу взять интеграл можно
было сразу взять интеграл 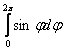 и получить ноль
(т.к. во внутренних интегралах от «фи» ничего не зависит), но такое решение вряд ли одобрят рецензенты. Тем не менее, оно
встречается. и получить ноль
(т.к. во внутренних интегралах от «фи» ничего не зависит), но такое решение вряд ли одобрят рецензенты. Тем не менее, оно
встречается.
Простенькая область и сакральный результат:
Пример 47
Вычислить интеграл 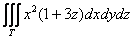 по телу по телу 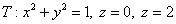
Решаем самостоятельно. Примерный образец чистового оформления задания в конце книги, оно почти устное.
Но этим всё дело не ограничивается! Читаем дальше:
 2.5. Тройной интеграл в сферических координатах 2.5. Тройной интеграл в сферических координатах
 2.3. Тройной интеграл в цилиндрических координатах 2.3. Тройной интеграл в цилиндрических координатах
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
|

 Научись решать за пару дней!
Научись решать за пару дней! Сверху тело ограничено плоскостью
Сверху тело ограничено плоскостью 
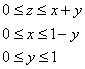
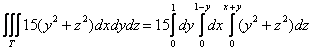
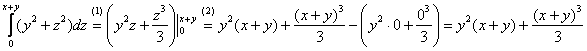
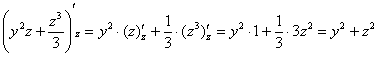 , что и хотелось увидеть.
, что и хотелось увидеть.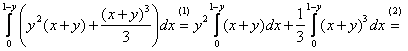
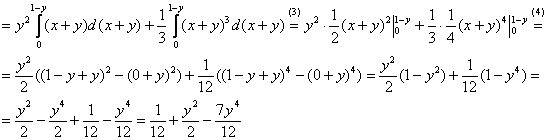
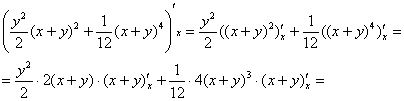
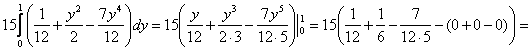
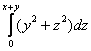 получена сумма
получена сумма  Решение:
область интегрирования ограничена шестью плоскостями и представляет собой прямоугольный параллелепипед:
Решение:
область интегрирования ограничена шестью плоскостями и представляет собой прямоугольный параллелепипед: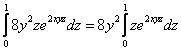 , который нужно
брать по частям. Аналогичная история, если в первую очередь интегрировать по «игрек»:
, который нужно
брать по частям. Аналогичная история, если в первую очередь интегрировать по «игрек»:  – тут даже дважды по частям.
– тут даже дважды по частям.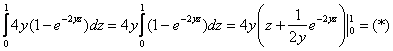
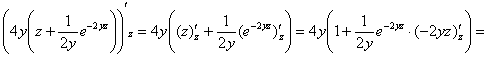
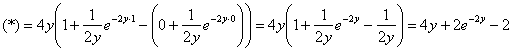
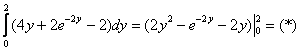

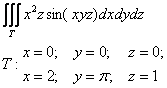
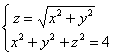 – подставим
– подставим 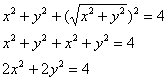

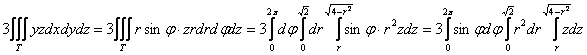
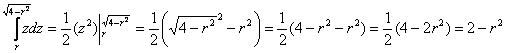
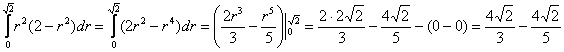
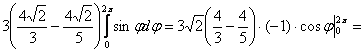
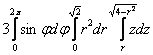 можно
было сразу взять интеграл
можно
было сразу взять интеграл 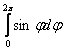 и получить ноль
(т.к. во внутренних интегралах от «фи» ничего не зависит), но такое решение вряд ли одобрят рецензенты. Тем не менее, оно
встречается.
и получить ноль
(т.к. во внутренних интегралах от «фи» ничего не зависит), но такое решение вряд ли одобрят рецензенты. Тем не менее, оно
встречается. 2.5. Тройной интеграл в сферических координатах
2.5. Тройной интеграл в сферических координатах 2.3. Тройной интеграл в цилиндрических координатах
2.3. Тройной интеграл в цилиндрических координатах