|
Блиц-курс – Кратные и криволинейные интегралы |
1.6. Центр тяжести плоской фигурыЭто популярное физическое приложение двойного интеграла. О центре тяжести плоской фигуры я рассказывал ещё в курсе аналитической геометрии, и сейчас мы на пальцах повторим, что это такое. Вырежьте из тонкого куска картона произвольную фигуру, какую захотИте. …Есть? Поднимите указательный палец строго вверх J. Теперь положите картонку на палец и добейтесь того, чтобы она не сваливалась. Эта точка картонной фигуры – и есть её центр тяжести. В студенческой практике для решения, как правило, предлагается простейший случай – плоская ограниченная однородная фигура,
то есть фигура постоянной физической плотности – стеклянная, деревянная, оловянная Первое правило и простейший пример: если у плоской фигуры есть центр симметрии, то он является центром тяжести данной фигуры. Например, центр круглой или квадратной однородной пластины. Логично и по-житейски понятно – масса такой фигуры «справедливо распределена во все стороны» относительно центра. Однако в суровых реалиях вам вряд ли подкинут такую халяву, и поэтому на помощь придётся привлечь серьёзный математический аппарат: Координаты
И наиболее компактная запись: Интеграл Примечание-справка: для плоской ограниченной неоднородной фигуры, плотность которой задана функцией На формулах, собственно, вся новизна и заканчивается, остальное – это ваше умение решать двойные интегралы, кстати, сейчас предоставляется прекрасная возможность потренироваться и усовершенствовать свою технику. А совершенству, как известно, нет предела: …или есть? :) Пример 29 Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями Решение: линии здесь элементарны: В нашем случае фигура симметрична относительно прямой Также обратите внимание, что по вертикали центр тяжести смещён ближе к оси абсцисс, поскольку там фигура более массивна. Полезная рекомендация: ещё до вычислений постарайтесь определить примерное расположение центра тяжести «на глазок» – это
поможет проверить полученные значения …Да, возможно, ещё не все до конца поняли, что такое центр тяжести: пожалуйста, поднимите вверх указательный палец и
мысленно поставьте на него заштрихованную «подошву» точкой Координаты центра тяжести фигуры найдём по формулам Внимание! Определяемся с наиболее выгодным порядком обхода один раз – и используем его для всех двойных интегралов! А их тут будет три штуки: 1) Сначала вычислим площадь фигуры. Ввиду относительной простоты интеграла решение можно оформить «одной строкой», главное,
не запутаться в вычислениях: 2) Иксовая координата Следующие два примера для самостоятельного решения. Попроще: Пример 30 Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями И посложнее: Пример 31 Найти центр тяжести однородной плоской фигуры, ограниченной линиями И это как раз тот случай, когда вроде бы выполнены предпосылки для перехода к полярной системе координат, но в результате получаются настолько харкордные интегралы, что уж лучше решать в декартовых координатах. Примерные образцы решений в конце книги. Но, разумеется, есть задачи, где решение в полярных координатах оправдано. Желающие могут в качестве тренировки найти
центр тяжести фигуры из Примера 23, тем более, там уже найдена площадь. Верный ответ Ну а сейчас пришло время немного отдохнуть и повысить ставки:
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за пару дней!
Научись решать за пару дней!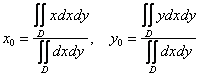 , их также можно
записать так:
, их также можно
записать так: 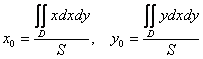 , где
, где 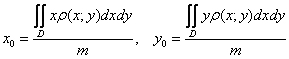 , где
, где 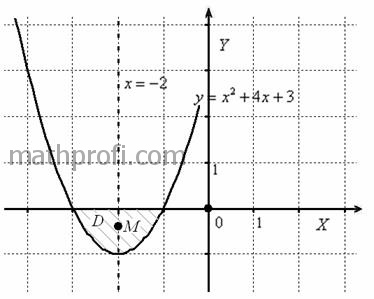
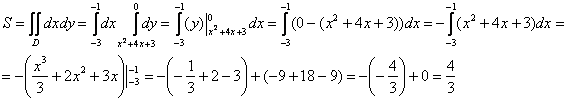

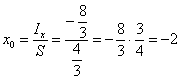 , что и требовалось получить.
, что и требовалось получить.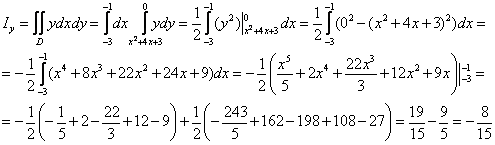
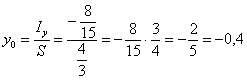 , что
очень и очень похоже на правду. На заключительном этапе отмечаем на чертеже точку
, что
очень и очень похоже на правду. На заключительном этапе отмечаем на чертеже точку  2. Тройные инетгралы
2. Тройные инетгралы  1.5. Как вычислить двойной интеграл в полярных координатах?
1.5. Как вычислить двойной интеграл в полярных координатах?