3. Криволинейные интегралы
И чтобы у вас сразу отлегло от сердца: криволинейные интегралы – это всего лишь однократные интегралы. Они похожи на «обычные» определённые интегралы.
Уже из самого названия нетрудно догадаться, что путём интегрирования криволинейных интегралов являются кривые линии (в общем случае).
Итак, паркет вашей комнаты – это координатная плоскость 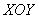 , в углу стоИт , в углу стоИт
эльф ось 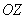 , а сверху «зависло» расправленное одеяло, заданное функцией , а сверху «зависло» расправленное одеяло, заданное функцией 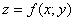 . .
Возьмите в руки мел и начертите на полу под одеялом произвольную кривую 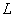 . Как вариант, у неё могут быть углы – такая линия называется кусочно-гладкой. Можно изобразить даже ломаную. ВажнА спрямляемость и непрерывность пути интегрирования. Теперь суть: . Как вариант, у неё могут быть углы – такая линия называется кусочно-гладкой. Можно изобразить даже ломаную. ВажнА спрямляемость и непрерывность пути интегрирования. Теперь суть:
Представьте, что от одеяла осталась всего лишь нитка, лежащая над кривой 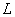 . Вертикальная поверхность, расположенная между кривой «эль» на полу и этой «ниткой» представляет собой фрагмент криволинейного цилиндра. …Получилась такая стоячая изогнутая ширма. …Представили? Отлично! . Вертикальная поверхность, расположенная между кривой «эль» на полу и этой «ниткой» представляет собой фрагмент криволинейного цилиндра. …Получилась такая стоячая изогнутая ширма. …Представили? Отлично!
3.1. Криволинейный интеграл первого рода
имеет вид 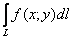 и по модулю* равен площади и по модулю* равен площади 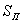 данной «ширмы» (фрагмента криволинейного цилиндра). данной «ширмы» (фрагмента криволинейного цилиндра).
* Если график 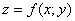 целиком или бОльшей частью расположен ниже плоскости целиком или бОльшей частью расположен ниже плоскости 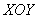 , то площадь получится со знаком «минус». , то площадь получится со знаком «минус».
В частности, если подынтегральная функция задаёт плоскость 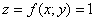 , то криволинейный интеграл равен площади «ленты» единичной высоты, а также и длине самой линии интегрирования: , то криволинейный интеграл равен площади «ленты» единичной высоты, а также и длине самой линии интегрирования: 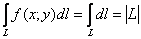 . .
…Чего только не придумаешь, чтобы не делать чертежей :)
Значок 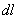 называют дифференциалом дуги кривой называют дифференциалом дуги кривой 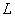 . Во многих источниках его обозначают через . Во многих источниках его обозначают через 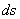 , но, на мой взгляд, это не слишком удачный выбор. , но, на мой взгляд, это не слишком удачный выбор.
Если на плоскости 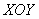 вместо кривой начертить отрезок прямой, то получится не что иное, как плоская криволинейная трапеция, параллельная оси вместо кривой начертить отрезок прямой, то получится не что иное, как плоская криволинейная трапеция, параллельная оси 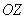 . Соответствующий интеграл хоть и каламбурно, но с полным правом можно назвать «прямолинейным», и это двоюродный брат определённого интеграла. . Соответствующий интеграл хоть и каламбурно, но с полным правом можно назвать «прямолинейным», и это двоюродный брат определённого интеграла.
 3.1.1. Как вычислить криволинейный интеграл 1-го рода? 3.1.1. Как вычислить криволинейный интеграл 1-го рода?
 2.6.2. Центр тяжести тела 2.6.2. Центр тяжести тела
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
|

 Научись решать за пару дней!
Научись решать за пару дней! 3.1.1. Как вычислить криволинейный интеграл 1-го рода?
3.1.1. Как вычислить криволинейный интеграл 1-го рода? 2.6.2. Центр тяжести тела
2.6.2. Центр тяжести тела