|
Блиц-курс – Кратные и криволинейные интегралы |
3.6. Физический смысл криволинейных интеграловСначала совсем кратко, почти в качестве оффтопа 3.6.1. Смысл интеграла 1-го родаКриволинейный интеграл первого рода по кусочно-гладкой дуге Примера не будет ввиду крайней редкости этой задачи, поэтому сразу суть криволинейного интеграла 2-го рода и гвоздь программы: 3.6.2. Работа векторного поляПусть материальная точка под воздействием силы векторного
поля Давайте разбираться. Приведу не совсем строгий, но зато вполне понятный пример: представьте, что у вас на столе лежит
плоский и достаточно тонкий магнит. Из жизненного опыта все хорошо знают, что чем ближе поднести к нему какую-нибудь железку,
тем сильнее она будет притягиваться. В физике это «сильнее» измеряется векторной величиной под названием напряжённость
магнитного поля: И в самом деле, если мы начнём подставляться координаты Теперь недалеко от магнита бросим железную пылинку, которая под действием силы магнитного поля проделает путь
И совсем понятный пример находится у многих под рукой, а именно компьютерная мышка – переместите её по произвольной траектории. Сила ваших мускулов совершила работу по перемещению мыши. Однако обывательское и физическое понимание работы отличаются, и к этому вопросу я вернусь буквально через несколько строк: Пример 64 Вычислить непосредственно и с помощью формулы Грина работу векторного поля Решаем самостоятельно! Краткое решение и ответ в конце книги. И не такое оно, между прочим, простое, как может показаться ;-) Не удивляйтесь, если работа будет получаться отрицательной – знаки «плюс» и «минус» указывают направление действия силы.
Так, если вы переместите мышь вправо, то, условно говоря, совершите работу Вы поработали? Безусловно. Хотя и не перетрудились =) Но с точки зрения физики никакой работы не
совершено! И действительно, работа по замкнутому контуру составила Если интеграл по замкнутому контуру равен нулю, то соответствующее векторное
поле называют потенциальным. Проверим, будет ли оно таковым в Примере 64:
Кстати, такое задание иногда встречается: проверить будет ли данное поле потенциальным и если да, то найти его потенциал. Напоминаю, что для нахождения потенциальной функции нужно решить дифференциальное уравнение в полных дифференциалах. Ну а как решить эту задачу в пространственном случае, я рассказываю на сайте, а другой теме – теория поля. …Да, начинается полный хардкор :). И в заключение курса мы как раз немного поговорим
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за пару дней!
Научись решать за пару дней!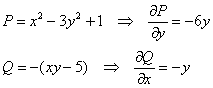
 3.7. О криволинейных интегралах в пространстве
3.7. О криволинейных интегралах в пространстве 3.5. Формула Грина – Остроградского
3.5. Формула Грина – Остроградского