|
Блиц-курс – Кратные и криволинейные интегралы |
3.4. Криволинейный интеграл по замкнутому контуруПродолжаем решать криволинейные интегралы 2-го рода. Новизна будет состоять в особенности пути интегрирования, а именно в его замкнутости. Наверное, всем интуитивно понятно, что это значит – встаньте с места и прогуляйтесь, как вам захочется. После чего вернитесь в исходную точку. Это и есть замкнутый контур. В рамках данной книги я рассмотрю элементарные маршруты без самопересечений, такие как окружность, треугольник, квадрат и т.п. Криволинейный интеграл по замкнутому контуру На практике чаще всего встречается первый вариант, который принято называть положительным направлением обхода контура. Впрочем, чтобы послать по контуру – стрелка не обязательна:) Пример 62 Вычислить интеграл Решение: Слушаемся и повинуемся:) В силу свойства аддитивности, криволинейный интеграл по контуру И теперь, вы, наверное, поняли, что нас ждёт дальше: 1) Вычислим интеграл по дуге В соответствии с направлением, Желающие могут выполнить проверку: выразить нужный кусок параболы: 2) Вычислим интеграл по отрезку 3) И, наконец, интеграл по фрагменту Осталось просуммировать три куска и получить результат по всему контуру: Ответ: Если контур обойти по часовой стрелке, то получится противоположное значение: Другой очевидный факт состоит в том, что если мы начнём свой путь из любой другой точки контура и совершим «оборот» (в том или ином направлении), то значение интеграла не изменится. Что можно сказать по поводу выполненного задания? Решение хорошее, решение логичное, однако у него есть существенный недостаток. Оно длинное. …Но это не беда! Если нет беды с двойными интегралами :). Для простых контуров существует:
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за пару дней!
Научись решать за пару дней!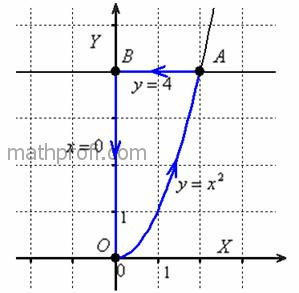
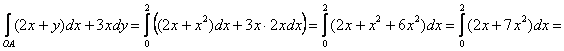
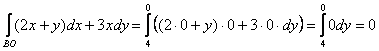
 3.5. Формула Грина – Остроградского
3.5. Формула Грина – Остроградского 3.3.2. Если линия задана параметрически
3.3.2. Если линия задана параметрически