3.5. Формула Грина – Остроградского
Или, как её чаще называют – просто формула Грина, которую обычно записывают для положительного направления обхода контура:
 , где , где 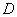 – замкнутая область, ограниченная контуром – замкнутая область, ограниченная контуром 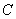 . .
Примечание: функции 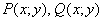 должны быть определены и непрерывны в области должны быть определены и непрерывны в области 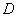 и, кроме того, иметь в ней непрерывные частные
производные и, кроме того, иметь в ней непрерывные частные
производные 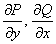 . .
! Замечание: буквы 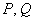 –
стандартны, не меняем их и не переставляем! –
стандартны, не меняем их и не переставляем!
Решим наш интеграл 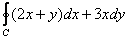 по
формуле Грина. Сначала найдём частные производные: по
формуле Грина. Сначала найдём частные производные:
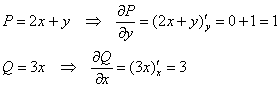
Для наглядности скопирую чертёж сверху:
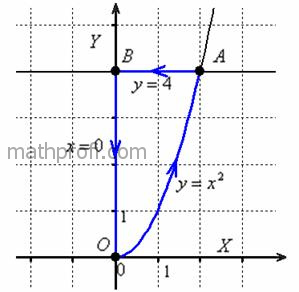
Область 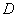 ограничена контуром ограничена контуром
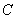 (синими линиями) и мы
выбираем её привычный порядок обхода: (синими линиями) и мы
выбираем её привычный порядок обхода: 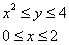 . В результате чего получаем: . В результате чего получаем:
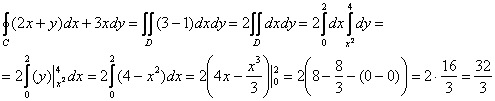
Как видите, решение сильно сократилось, а иногда оно сокращается просто фантастически! Чему посвящён следующий пример:
Пример 63
Вычислить криволинейный интеграл 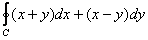 по окружности по окружности 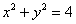 : а) непосредственно, б) по формуле Грина. : а) непосредственно, б) по формуле Грина.
Решение: естественно, здесь не нужно мучиться с полуокружностями и их уравнениями 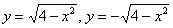 (хотя можно) – гораздо проще
представить уравнение окружности (хотя можно) – гораздо проще
представить уравнение окружности 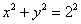 в параметрической форме, которая уже неоднократно встречалась
ранее: в параметрической форме, которая уже неоднократно встречалась
ранее: 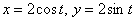
В условии ничего не сказано о направлении обхода контура, но пункт «бэ» толсто
намекает, что лучше двигаться против часовой стрелки. К тому же, традиционное возрастание параметра  как раз и обеспечивает «виток» именно в этом
направлении: как раз и обеспечивает «виток» именно в этом
направлении:
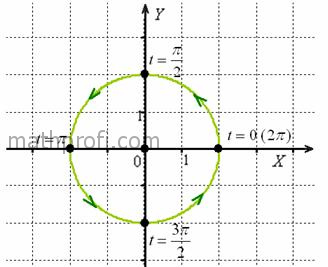
Чертёж, к слову, был вовсе не обязателен, и ввиду простоты контура можно было обойтись и без него. Однако не в этот раз –
пожалуйста, ХОРОШО запечатлейте эту картинку в своём сознании!
а) Вычислим криволинейный интеграл непосредственно. Алгоритм решения обычный – «начинку»
интеграла нужно «заправить» буквой «тэ». Найдём дифференциалы:
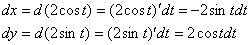
и подставим 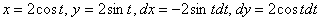 в
подынтегральное выражение. Чтобы не запутаться рекомендую оформлять преобразования «столбиком»: в
подынтегральное выражение. Чтобы не запутаться рекомендую оформлять преобразования «столбиком»:
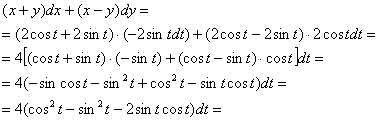
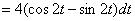 , на последнем шаге
использованы формулы двойного угла, надеюсь, вы их не забудете в любом состоянии =) , на последнем шаге
использованы формулы двойного угла, надеюсь, вы их не забудете в любом состоянии =)
Таким образом, криволинейный интеграл:
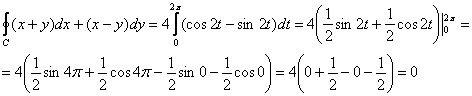
б) Вычислим интеграл по формуле Грина:
 , где , где  – замкнутая область, ограниченная контуром – замкнутая область, ограниченная контуром
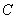 . В данном случае это
круг радиуса 2. Но возиться с полуокружностями не придётся и здесь! – поскольку: . В данном случае это
круг радиуса 2. Но возиться с полуокружностями не придётся и здесь! – поскольку:
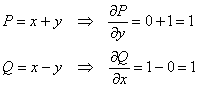
и сбылась мечта тунеядца:)
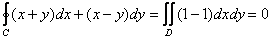
Ответ: 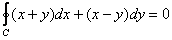
И это не только приятный, но ещё и крайне интересный случай. Если криволинейный интеграл по замкнутому контуру равен нулю,
то речь заходит об очень крутом свойстве! Даже о нескольких крутых свойствах. Должен предупредить, что сейчас я буду вольно
пересказывать теоремы математического анализа, и если вы учитесь основательно, то обязательно загляните в 3-й том Фихтенгольца
(например).
Рассмотрим две произвольные точки области 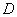 (круга). Очевидно, что их можно соединить бесчисленным
количеством кусочно-гладких маршрутов, не выходящих за пределы области. Так вот – какой бы из этих путей мы ни
выбрали, то во всех случаях криволинейный интеграл будет равняться одному и тому же
значению! (круга). Очевидно, что их можно соединить бесчисленным
количеством кусочно-гладких маршрутов, не выходящих за пределы области. Так вот – какой бы из этих путей мы ни
выбрали, то во всех случаях криволинейный интеграл будет равняться одному и тому же
значению!
Но это только «вершки». Поскольку функции 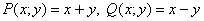 определены и непрерывны во всех точках плоскости определены и непрерывны во всех точках плоскости
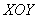 , то то же самое справедливо и
для любых двух точек плоскости! То есть, мы можем зафиксировать вообще любые две точки (какие понравятся) и составить
бесконечно много кусочно-гладких маршрутов между ними. И криволинейные интегралы по всем этим маршрутам будут равны
одному и тому же числу! В таких случаях говорят, что криволинейный интеграл не зависит от пути интегрирования,
а зависит только от начальной и конечной точки. , то то же самое справедливо и
для любых двух точек плоскости! То есть, мы можем зафиксировать вообще любые две точки (какие понравятся) и составить
бесконечно много кусочно-гладких маршрутов между ними. И криволинейные интегралы по всем этим маршрутам будут равны
одному и тому же числу! В таких случаях говорят, что криволинейный интеграл не зависит от пути интегрирования,
а зависит только от начальной и конечной точки.
Более того, если мы возьмём произвольный замкнутый кусочно-гладкий контур 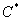 в плоскости в плоскости 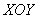 , то интеграл по любому такому контуру будет равен нулю: , то интеграл по любому такому контуру будет равен нулю:
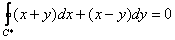
Вернёмся к только что разобранному примеру и рассмотрим произвольную пару точек, лежащую внутри круга 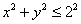 – проще всего взять точки – проще всего взять точки 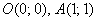 . Теперь вычислим криволинейный
интеграл двумя способами: . Теперь вычислим криволинейный
интеграл двумя способами:
1) По отрезку 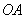 прямой прямой 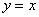 . Тут всё элементарно: . Тут всё элементарно: 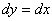 и: и:
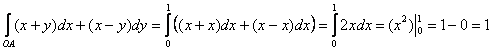
2) По дуге 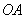 параболы параболы 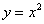 . В этом случае . В этом случае 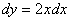 и: и:
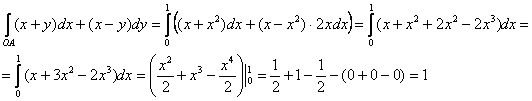
Самостоятельно вычислите этот же интеграл по дуге 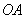 кубической параболы кубической параболы 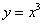 . Получится единица. Или по какой-нибудь простенькой ломаной,
например, по ломаной . Получится единица. Или по какой-нибудь простенькой ломаной,
например, по ломаной 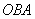 , где , где 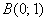 . Тоже получится единица! Возьмите
точку . Тоже получится единица! Возьмите
точку 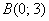 вне круга и снова
получИте свою законную единицу! И вообще – если выбрать любой кусочно-гладкий путь от точки вне круга и снова
получИте свою законную единицу! И вообще – если выбрать любой кусочно-гладкий путь от точки 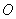 до точки до точки 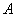 , то криволинейный интеграл во всех
случаях будет равняться единице! Сколь бы долгим и запутанным ни был маршрут в плоскости , то криволинейный интеграл во всех
случаях будет равняться единице! Сколь бы долгим и запутанным ни был маршрут в плоскости 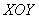 , сколько бы он не самопересекался (да, даже так). , сколько бы он не самопересекался (да, даже так).
Иными словами, значение криволинейного интеграла не зависит от пути интегрирования. И, как я уже отметил
выше, в нашем примере можно взять вообще две любые точки плоскости 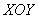 , и криволинейный интеграл не будет зависеть от пути интегрирования.
Напоминаю, что всё это последовало из того, что мы получили ноль хоть по какому-то замкнутому контуру (по
окружности в нашем примере), а также из того факта, что функции , и криволинейный интеграл не будет зависеть от пути интегрирования.
Напоминаю, что всё это последовало из того, что мы получили ноль хоть по какому-то замкнутому контуру (по
окружности в нашем примере), а также из того факта, что функции 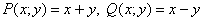 непрерывны всюду. непрерывны всюду.
Но открытия только начинаются!
Если 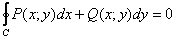 , то
подынтегральное выражение является полным
дифференциалом некоторой функции двух переменных , то
подынтегральное выражение является полным
дифференциалом некоторой функции двух переменных 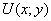 . Данная функция называется потенциальной или просто потенциалом. Как
её найти? Очень просто. Нужно решить . Данная функция называется потенциальной или просто потенциалом. Как
её найти? Очень просто. Нужно решить 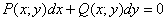 – дифференциальное уравнение в полных
дифференциалах. – дифференциальное уравнение в полных
дифференциалах.
Для «начинки» нашего нулевого интеграла 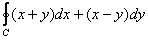 таковой функцией является: таковой функцией является: 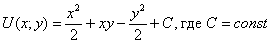
И в самом деле, её полный дифференциал:
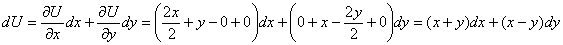 – в точности
подынтегральное выражение. – в точности
подынтегральное выражение.
Ну и, наверное, вы поняли, что равенство 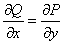 , которое обеспечивает ноль в формуле
Грина, есть не что иное, как равенство смешанных
производных 2-го порядка. , которое обеспечивает ноль в формуле
Грина, есть не что иное, как равенство смешанных
производных 2-го порядка.
Более того, для любых двух точек  и и 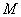 области области 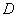 (и вообще всей плоскости (и вообще всей плоскости 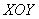 ) криволинейный интеграл ) криволинейный интеграл 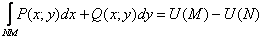 – равен постоянной величине, которая не зависит от пути
интегрирования. – равен постоянной величине, которая не зависит от пути
интегрирования.
Так, в нашем примере с точками 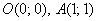 было совсем не обязательно перебирать множество маршрутов –
достаточно найти потенциальную функцию было совсем не обязательно перебирать множество маршрутов –
достаточно найти потенциальную функцию 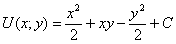 (решив ДУ в полных дифференциалах) и
вычислить криволинейный интеграл по формуле: (решив ДУ в полных дифференциалах) и
вычислить криволинейный интеграл по формуле:
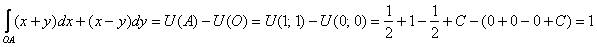
Разность 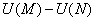 называют разностью
потенциалов, и я так вижу, у физиков уже появился здоровый блеск в глазах ^ : ^ Поэтому не буду томить вас ожиданием и быстро
перейду к следующему параграфу: называют разностью
потенциалов, и я так вижу, у физиков уже появился здоровый блеск в глазах ^ : ^ Поэтому не буду томить вас ожиданием и быстро
перейду к следующему параграфу:
 3.6. Физический смысл криволинейных интегралов 3.6. Физический смысл криволинейных интегралов
 3.4. Криволинейный интеграл по замкнутому контуру 3.4. Криволинейный интеграл по замкнутому контуру
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
|

 Научись решать за пару дней!
Научись решать за пару дней!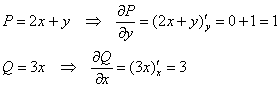

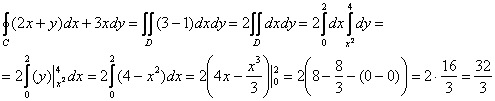

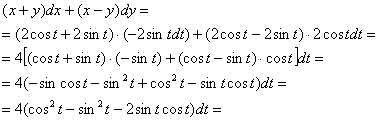
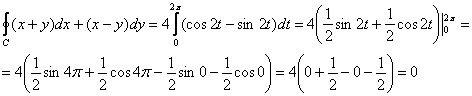
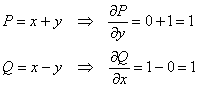
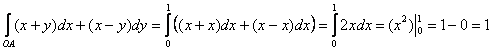
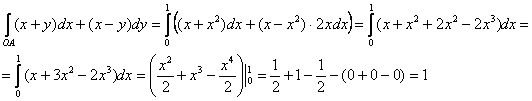
 3.6. Физический смысл криволинейных интегралов
3.6. Физический смысл криволинейных интегралов 3.4. Криволинейный интеграл по замкнутому контуру
3.4. Криволинейный интеграл по замкнутому контуру