|
Блиц-курс – Кратные и криволинейные интегралы |
3.3. Криволинейные интегралы второго родаВ этом курсе я почти не освещал теорию, но тут немножко надо, постарайтесь понять хотя бы примерно :). «Реалити-шоу» точно такое же. Отличие будет в способе интегрирования. Если
в интеграле Но в большинстве задач приходится иметь дело с так называемой общей формой криволинейного интеграла от двух
функций: С практической точки зрения будут важнЫ те же свойства
линейности и аддитивности, а также тот факт, что: криволинейный интеграл 2-го рода зависит от направления
интегрирования, при этом: С чисто формальной точки зрения криволинейный интеграл 2-го рода «опознаётся» по наличию в подынтегральном
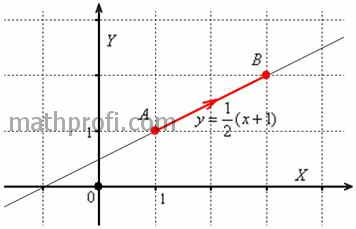
выражении дифференциалов Пример 56 Вычислить криволинейный интеграл Решение: на первом шаге нам нужно найти уравнение прямой, которая содержит
отрезок Несмотря на то, что линия интегрирования весьма простА, по условию требуется выполнить чертёж: Также всегда обращайте внимание на следующую вещь: каждая точка линии Иногда авторы задачников и методичек недоглядывают за этим моментом, в результате чего получается невразумительное решение, где ответ, например, может оказаться бесконечным.
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за пару дней!
Научись решать за пару дней!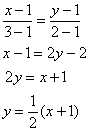
 3.3.1. Как вычислить криволинейный интеграл 2-го рода?
3.3.1. Как вычислить криволинейный интеграл 2-го рода? 3.2. Важные свойства криволинейных интегралов
3.2. Важные свойства криволинейных интегралов