|
Блиц-курс – Кратные и криволинейные интегралы |
3.7. О криволинейных интегралах в пространствеА почему нет? Никто же не запрещает интегрировать по пространственным кривым. Все только разрешают =) На самом деле я мог бы начать и с них, но, во-первых, такие задачи значительно реже встречаются на практике, и, во-вторых, возникла бы неслабая путаница. Пространственная кривая, как правило, задаётся параметрическими уравнениями Так, например, криволинейный интеграл 1-го рода, рассчитывается по формуле: Криволинейный интеграл 2-го рода запишется в виде: Осталось подтвердить свою догадку решением заключительного примера, решаем торжественно, решаем с энтузиазмом, решаем самостоятельно: Пример 65 Вычислить криволинейный интеграл Решение и ответ задачи в полной версии книги. Аналогично – предложенный криволинейный интеграл можно интерпретировать, как работу
трёхмерного векторного поля Следует добавить, что работа – есть «главный» физический смысл криволинейного интеграла второго рода, но далеко не единственный. Криволинейные интегралы нашли широкое применение в физике, с помощью них можно подсчитать много других величин. И, к слову, термин «поле» – он не физический, а относится именно к математике! Силовые же физические поля – лишь частные примеры. И я вас поздравляю! С дополнительной, в том числе теоретической информацией можно ознакомиться в соответствующем разделе портала mathprofi.ru, а также в учебной литературе, в частности, рекомендую: К.А. Бохан 2-й том, Г.М. Фихтенгольц, 3-й том Для тех, кто заинтересовался – есть продолжение, а именно, поверхностные интегралы. Сложновато, но подъёмно! ;) Также логическим продолжением темы является теория поля. Желаю успехов!
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за пару дней!
Научись решать за пару дней!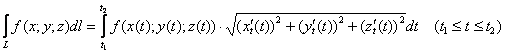 , и его
, и его  3.6. Физический смысл криволинейных интегралов
3.6. Физический смысл криволинейных интегралов