3.1.1. Как вычислить криволинейный интеграл первого рода?
Пусть точки 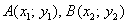 являются концами
линии являются концами
линии 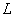 , а сама она задана
функцией одной переменной , а сама она задана
функцией одной переменной 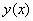 (в плоскости (в плоскости 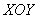 ). Тогда криволинейный
интеграл первого рода можно свести к определённому интегралу по следующей
формуле: ). Тогда криволинейный
интеграл первого рода можно свести к определённому интегралу по следующей
формуле:
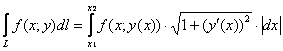
Формулу можно расписать подробно, без модуля при «дэ икс»:
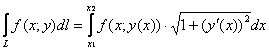 , если , если 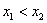 (стандартный случай) или (стандартный случай) или
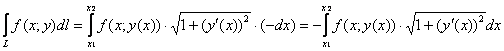 , если , если 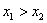 . .
В частности, при 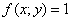 получается хорошо знакомая формула длины дуги кривой получается хорошо знакомая формула длины дуги кривой 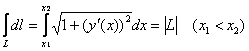 . …Вот так-то оно бывает – оказывается, криволинейные интегралы мы уже
решали! И теперь вам совсем не нужно решимости:) . …Вот так-то оно бывает – оказывается, криволинейные интегралы мы уже
решали! И теперь вам совсем не нужно решимости:)
Пример 53
Вычислить интеграл 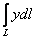 от точки от точки 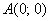 до точки до точки 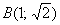 , если кривая , если кривая 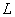 задана уравнением задана уравнением 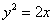
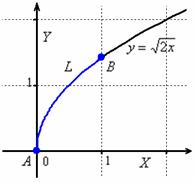
Решение: перед нами каноническое уравнение параболы, и коль скоро в условии дана точка 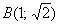 , то речь идёт о её верхней ветке: , то речь идёт о её верхней ветке: 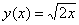 . И вы можете даже не знать, как выглядит
эта кривая. Здесь важно, что интегрирование проводится от точки . И вы можете даже не знать, как выглядит
эта кривая. Здесь важно, что интегрирование проводится от точки 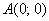 до точки до точки 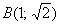 , а посему , а посему 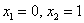 . Таким образом, у нас наиболее распространённый случай . Таким образом, у нас наиболее распространённый случай 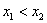 , следовательно, нужно использовать формулу: , следовательно, нужно использовать формулу:
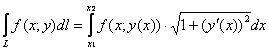 . .
Сначала удобно найти производную: 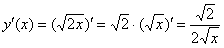 и сразу же упростить корень: и сразу же упростить корень: 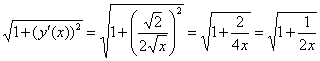 . .
Так как 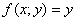 и и 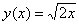 , то , то 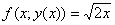 – грубо говоря, на данном шаге мы избавляемся от «игреков». – грубо говоря, на данном шаге мы избавляемся от «игреков».
Предварительная подготовка завершена, пользуемся формулой:
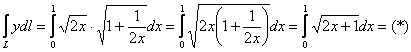
здесь можно провести замену переменной, но гораздо сподручнее подвести подкоренное выражение под знак
дифференциала и обойтись без перехода к новым пределам интегрирования:
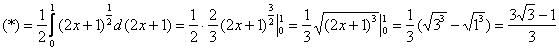
Ответ: 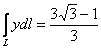
Если вычислить тот же самый интеграл в противоположном направлении – от точки 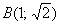 до точки до точки 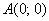 , то результат не изменится. В этом случае пределы интегрирования
поменяются местами , то результат не изменится. В этом случае пределы интегрирования
поменяются местами 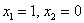 , и коль скоро , и коль скоро
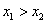 , то мы пользуемся второй
формулой: , то мы пользуемся второй
формулой: 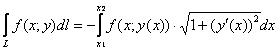 , в нашем случае: , в нашем случае:
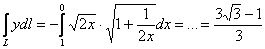
По существу, тут работает свойство 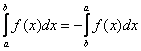 определённого интеграла. определённого интеграла.
Таким образом, криволинейный интеграл 1-го рода не зависит от направления интегрирования: 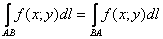 . .
В этой связи типовая задача, как правило, формулируется «нейтрально»: вычислить интеграл 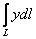 вдоль дуги параболы вдоль дуги параболы 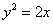 , расположенной между точками , расположенной между точками 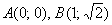 . Иными словами, совершенно не важно, какая из точек является началом,
а какая – концом кривой. . Иными словами, совершенно не важно, какая из точек является началом,
а какая – концом кривой.
Следует отметить, что криволинейный интеграл можно вычислить и другим способом. Поскольку буква «игрек» ничем не хуже
«икса», то для вычисления криволинейного интеграла 1-го рода справедлива «зеркальная» формула (тривиальный вариант
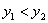 ): ):
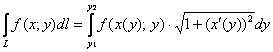 , где , где 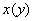 – обратная функция, выражающая линию – обратная функция, выражающая линию 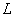 . .
С параболой никаких проблем 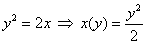 , ,
и производной – тем более: 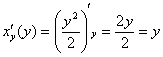
При переходе от 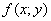 к к 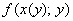 мы должны избавиться от всех «иксов»,
однако функция мы должны избавиться от всех «иксов»,
однако функция 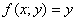 от них не
зависит, а значит, делать ничего не нужно. от них не
зависит, а значит, делать ничего не нужно.
И, учитывая, что для «игрековых» координат точек 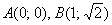 справедливо неравенство справедливо неравенство 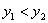 , доводим решение до того же самого результата: , доводим решение до того же самого результата:

В чём состоит геометрический смысл разобранной задачи? На плоскости 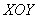 между точками между точками 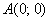 и и 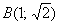 находится кусок параболы находится кусок параболы 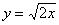 , через который проходит «одноимённый» параболический
цилиндр , через который проходит «одноимённый» параболический
цилиндр 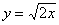 параллельно оси параллельно оси
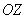 . .
Этот цилиндр «высекает» из плоскости 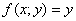 пространственную «ниточку» (выше плоскости пространственную «ниточку» (выше плоскости 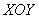 ). ).
Криволинейный интеграл 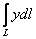 численно равен площади численно равен площади 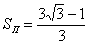 фрагмента параболического цилиндра, который расположен между
куском параболы и этой «ниткой». ...Вроде всё понятно…. фрагмента параболического цилиндра, который расположен между
куском параболы и этой «ниткой». ...Вроде всё понятно….
Как я уже отмечал, криволинейный интеграл может получиться отрицательным – это означает, что фрагмент полностью или бОльшей
частью лежит ниже плоскости 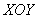 .
Не удивляйтесь и нулю (в каких случаях?). То есть, «всё как у нормальных интегралов» :) .
Не удивляйтесь и нулю (в каких случаях?). То есть, «всё как у нормальных интегралов» :)
Аналогичный пример для самостоятельного решения:
Пример 54
Вычислить интеграл 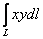 по дуге
окружности по дуге
окружности 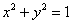 от точки от точки 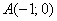 до точки до точки 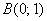 . Пояснить геометрический смысл полученного результата. . Пояснить геометрический смысл полученного результата.
Краткое решение с комментариями в конце книги – тот, кто правильно во всём разобрался, может считать себя «самоваром»
интегралов =)
Но этим практика не исчерпывается, ситуации бывают разные:
 3.1.2. Если линия задана параметрически 3.1.2. Если линия задана параметрически
 3.1. Криволинейные интегралы первого рода 3.1. Криволинейные интегралы первого рода
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
|

 Научись решать за пару дней!
Научись решать за пару дней!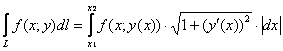
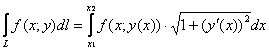 , если
, если 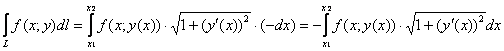 , если
, если 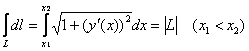 . …Вот так-то оно бывает – оказывается, криволинейные интегралы мы уже
решали! И теперь вам совсем не нужно решимости:)
. …Вот так-то оно бывает – оказывается, криволинейные интегралы мы уже
решали! И теперь вам совсем не нужно решимости:)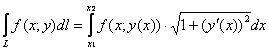 .
.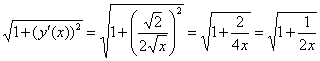 .
.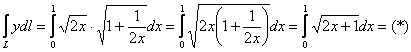
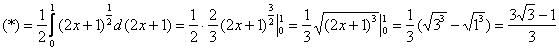
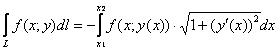 , в нашем случае:
, в нашем случае: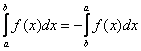 определённого интеграла.
определённого интеграла.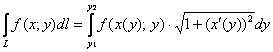 , где
, где 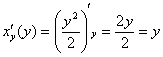


 3.1.2. Если линия задана параметрически
3.1.2. Если линия задана параметрически 3.1. Криволинейные интегралы первого рода
3.1. Криволинейные интегралы первого рода