2.3. Тройной интеграл в цилиндрических координатах
Цилиндрические координаты – это, по сути, полярные координаты в пространстве. В цилиндрической системе
координат положение произвольной точки 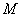 пространства определяется полярными координатами пространства определяется полярными координатами 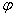 и и 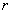 точки точки 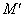 – проекции точки – проекции точки 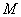 на плоскость на плоскость 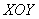 и аппликатой и аппликатой 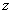 самой точки самой точки 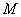 . .
Переход от трёхмерной декартовой системы к цилиндрической системе координат
осуществляется по следующим формулам:

Применительно к нашей теме преобразование выглядит следующим образом:
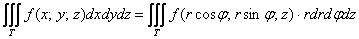
И, соответственно, в упрощённом случае, который мы рассматриваем сейчас:
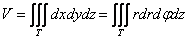
Главное, не забывать про дополнительный множитель «эр» и правильно расставлять полярные пределы интегрирования при
обходе проекции:
Пример 38
С помощью тройного интеграла вычислить объём тела, ограниченного поверхностями 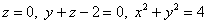 . Выполнить чертёж данного тела и его проекции на плоскость . Выполнить чертёж данного тела и его проекции на плоскость 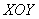 . .
Решение: придерживаемся того же порядка действий: в первую очередь рассматриваем уравнения, в которых
отсутствует переменная «зет». Оно здесь одно. Проекция цилиндрической поверхности 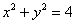 на плоскость на плоскость 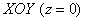 представляет собой одноимённую окружность представляет собой одноимённую окружность 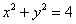 . Плоскости . Плоскости 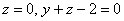 ограничивают искомое тело снизу и сверху и проецируются в круг ограничивают искомое тело снизу и сверху и проецируются в круг 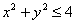 : :
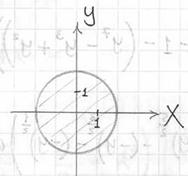
На очереди трёхмерный чертёж. Основная трудность состоит в построении плоскости 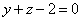 , которая пересекает цилиндр , которая пересекает цилиндр 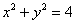 под «косым» углом, в результате чего получается эллипс. Уточним
данное сечение аналитически: для этого перепишем уравнение плоскости в функциональном виде под «косым» углом, в результате чего получается эллипс. Уточним
данное сечение аналитически: для этого перепишем уравнение плоскости в функциональном виде 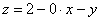 и вычислим значения функции («высоту») в напрашивающихся точках и вычислим значения функции («высоту») в напрашивающихся точках 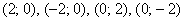 , которые лежат на границе проекции: , которые лежат на границе проекции: 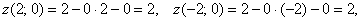 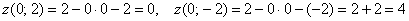 . Отмечаем найденные точки на чертеже и аккуратно (а не так, как я =))
соединяем их линией: . Отмечаем найденные точки на чертеже и аккуратно (а не так, как я =))
соединяем их линией:
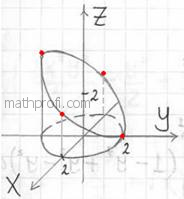
Проекция тела на плоскость 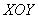 представляет собой круг, и это весомый аргумент в пользу перехода к
цилиндрической системе координат по формулам представляет собой круг, и это весомый аргумент в пользу перехода к
цилиндрической системе координат по формулам 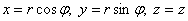 . .
Найдём уравнения поверхностей в цилиндрических координатах:
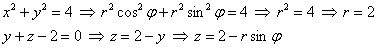
Теперь нужно выяснить порядок обхода тела. Сначала разберёмся с проекцией. Как определить её порядок обхода? ТОЧНО
ТАК ЖЕ, как и при вычислении двойных интегралов в полярных координатах. Здесь он
элементарен:
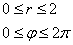
«Вертикальные» пределы интегрирования тоже очевидны – входим в тело через плоскость 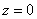 и выходим из него через плоскость и выходим из него через плоскость 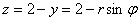 : :
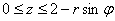
Перейдём к повторным интегралам:
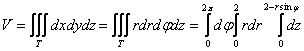 , при этом множитель «эр» сразу ставим в
«свой» интеграл. Веник как обычно ломаем по прутикам: , при этом множитель «эр» сразу ставим в
«свой» интеграл. Веник как обычно ломаем по прутикам:
1) 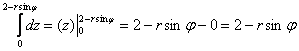
2) Сносим результат в следующий интеграл, не забывая, что там уже есть «эр»:
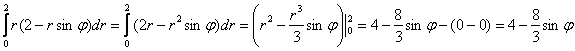
И ещё не забываем, что «фи» считается константой. Но это до поры до времени:
3) 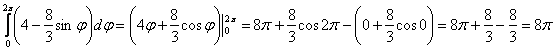
Ответ: 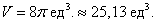
Похожее задание для самостоятельного решения:
Пример 39
Вычислить с помощью тройного интеграла объём тела, ограниченного поверхностями 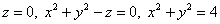 . Выполнить чертёж данного тела и его проекции на плоскость . Выполнить чертёж данного тела и его проекции на плоскость 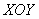 . .
Примерный образец чистового оформления в конце книги.
Обратите внимание, что в условиях задач ни слова не сказано о переходе к цилиндрической системе координат, и несведущий
человек будет «бодаться» с трудными интегралами в декартовых координатах. …А может и не будет – ведь есть третий, исконно
русский способ решения проблем =) …Но не после прочтения этой книги!
Пример 40
С помощью тройного интеграла найти объем тела, ограниченного поверхностями 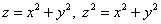
Скромно и со вкусом.
Решение: данное тело ограничено конической поверхностью 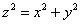 и эллиптическим параболоидом и эллиптическим параболоидом 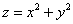 . Подготовленный читатель уже представил, как выглядит тело, но на практике
часто встречаются более сложные случаи, поэтому я проведу подробное аналитическое рассуждение. Сначала найдём линии, по
которым пересекаются поверхности. Составим и решим соответствующую систему: . Подготовленный читатель уже представил, как выглядит тело, но на практике
часто встречаются более сложные случаи, поэтому я проведу подробное аналитическое рассуждение. Сначала найдём линии, по
которым пересекаются поверхности. Составим и решим соответствующую систему:
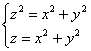
Из 1-го уравнения почленно вычтем второе:
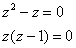
В результате получено два корня: 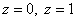
Подставим найденное значение 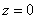 в любое
уравнение системы: в любое
уравнение системы:
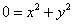 , откуда следует, что , откуда следует, что 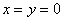 . .
Таким образом, корню 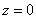 соответствует
единственная точка – начало координат. Естественно – ведь вершины рассматриваемых поверхностей совпадают. соответствует
единственная точка – начало координат. Естественно – ведь вершины рассматриваемых поверхностей совпадают.
Теперь подставим второй корень 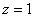 – тоже в
любое уравнение системы: – тоже в
любое уравнение системы:
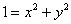
Каков геометрический смысл полученного результата? «На высоте» 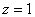 (в плоскости (в плоскости 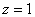 ) параболоид и конус пересекаются по окружности ) параболоид и конус пересекаются по окружности
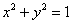 – единичного радиуса с центром в точке – единичного радиуса с центром в точке 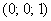 . При этом «чаша» параболоида вмещает в себя «воронку»
конуса, следовательно, образующие конической поверхности следует прочертить пунктиром (за исключением фрагмента
дальней от нас образующей, который виден с данного ракурса): . При этом «чаша» параболоида вмещает в себя «воронку»
конуса, следовательно, образующие конической поверхности следует прочертить пунктиром (за исключением фрагмента
дальней от нас образующей, который виден с данного ракурса):
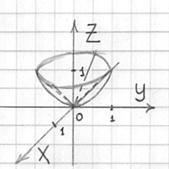
Проекцией тела на плоскость 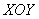 является
круг является
круг 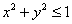 с центром в начале координат
радиуса 1, который я даже не удосужился изобразить ввиду очевидности данного факта. Кстати, и в двух предыдущих задачах можно
было обойтись без двухмерного чертежа, но там его требовало условие. с центром в начале координат
радиуса 1, который я даже не удосужился изобразить ввиду очевидности данного факта. Кстати, и в двух предыдущих задачах можно
было обойтись без двухмерного чертежа, но там его требовало условие.
При переходе к цилиндрическим координатам по формулам 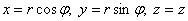 неравенство неравенство 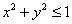 запишется в простейшем виде запишется в простейшем виде 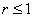 и с порядком обхода проекции никаких
проблем: и с порядком обхода проекции никаких
проблем:
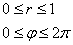
Найдём уравнения поверхностей в цилиндрической системе координат.
С параболоидом проблем нет вообще:
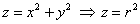
И с конусом их тоже нет. Так как в задаче рассматривается его верхняя часть, то из уравнения 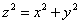 выражаем: выражаем: 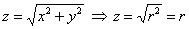
«Сканируем тело» вертикально, строго снизу вверх. Лучи света входят в него через эллиптический
параболоид 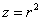 и выходят через
коническую поверхность и выходят через
коническую поверхность 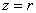 . Таким
образом, «вертикальный» порядок обхода тела: . Таким
образом, «вертикальный» порядок обхода тела:
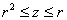
В результате: 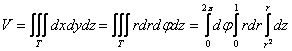
Остальное – дело несложной техники:
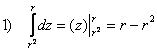
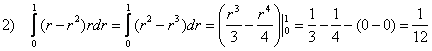
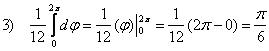
Ответ: 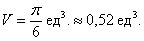
Не редкость, когда тело задаётся не ограничивающими его поверхностями, а множеством неравенств:
Пример 41
С помощью тройного интеграла вычислить объём заданного тела:
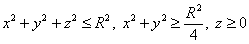 , где , где 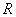 – произвольное положительное число. – произвольное положительное число.
Данная задача хоть и содержит параметр, но допускает выполнение точного чертежа, отражающего принципиальный вид тела.
Подумайте, как выполнить построение. Краткое решение и ответ – в конце книги.
 2.4. Как вычислить произвольный тройной интеграл? 2.4. Как вычислить произвольный тройной интеграл?
 2.2. Как вычислить объём тела с помощью тройного интеграла? 2.2. Как вычислить объём тела с помощью тройного интеграла?
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
|

 Научись решать за пару дней!
Научись решать за пару дней!


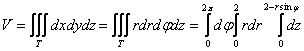 , при этом множитель «эр» сразу ставим в
«свой» интеграл. Веник как обычно ломаем по прутикам:
, при этом множитель «эр» сразу ставим в
«свой» интеграл. Веник как обычно ломаем по прутикам: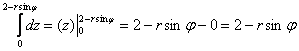
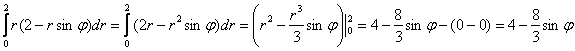
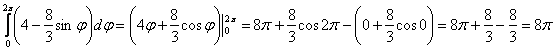
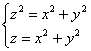

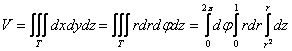
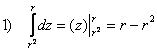
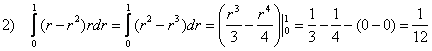
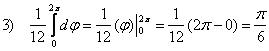
 2.4. Как вычислить произвольный тройной интеграл?
2.4. Как вычислить произвольный тройной интеграл? 2.2. Как вычислить объём тела с помощью тройного интеграла?
2.2. Как вычислить объём тела с помощью тройного интеграла?