|
Блиц-курс – Кратные и криволинейные интегралы |
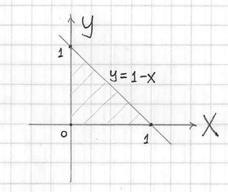
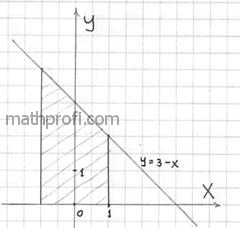
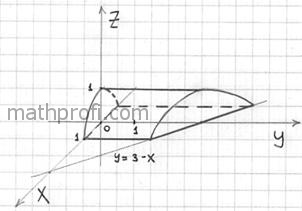
2.2. Как вычислить объём тела с помощью тройного интеграла?По формуле Пример 32 С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями Пожалуйста, перепишите на бумагу следующий список: Если Вы склоняетесь к общему ответу «скорее нет, чем да», то обязательно проработайте материалы по геометрии, которые я рекомендовал на предыдущей странице. Без этого дальше никуда. Решение: используем формулу Для того чтобы выяснить порядок обхода тела и перейти к повторным интегралам нужно (всё гениальное просто) понять, что это за тело. И такому пониманию во многих случаях здОрово способствуют чертежи. По условию, тело ограничено несколькими поверхностями. С чего начать построение? Предлагаю следующий порядок действий: Сначала изобразим параллельную ортогональную проекцию тела на координатную плоскость Коль скоро проецирование проводится вдоль оси – уравнение Исходя из вышесказанного, искомая проекция, скорее всего, представляет собой следующий треугольник: Обращаю особое внимание, что пока мы высказали лишь предположение о проекции и оговорки «скорее всего»,
«вероятнее всего» были не случайны. Дело в том, что проанализированы ещё не все поверхности и может статься так, что
какая-нибудь из них «оттяпает» часть треугольника. В качестве наглядного примера напрашивается сфера с центром в
начале координат радиусом мЕньшим единицы, например, сфера На втором этапе выясним, чем тело ограничено сверху, чем снизу и выполним пространственный чертёж. Возвращаемся к условию
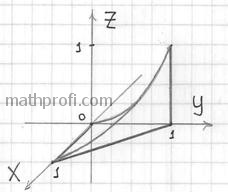
задачи и смотрим, какие поверхности остались. Уравнение Аккуратно изобразим фрагмент параболического цилиндра и искомое тело: Сначала определим порядок обхода проекции (при этом ГОРАЗДО УДОБНЕЕ использовать двумерный чертеж – см. выше). Это делается АБСОЛЮТНО ТАК ЖЕ, как и в двойных интегралах! Вспоминаем лазерную указку и «сканирование» плоской области. Выберем «традиционный» 1-й способ обхода: Далее берём в руки волшебный фонарик, смотрим на трёхмерный чертёж и строго снизу вверх просвечиваем
пациента. Лучи входят в тело через плоскость Перейдём к повторным интегралам: С интегралами вновь (ещё раз вновь) рекомендую разбираться по отдельности: 1) Начать следует с самого нутра – «зетового» интеграла: Подставим результат в «игрековый» интеграл: Что получилось? По существу решение свелось к двойному интегралу, и именно – к формуле 2) 3) Последний интеграл удобно взять методом подведения под знак дифференциала – ещё раз заостряю внимание на этом выгодном способе решения:
Ответ: Вычисления всегда можно записать и «одной строкой»:
Но с этим способом будьте осторожнее – выигрыш в скорости чреват потерей качества, и чем труднее пример, тем больше шансов допустить ошибку. Ответим на важный технический вопрос: Нужно ли делать чертежи, если условие задачи не требует их выполнения? Можно пойти четырьмя путями: 1) Изобразить проекцию и само тело. Это самый выигрышный вариант – если есть возможность выполнить два приличных чертежа, не ленитесь, делайте оба чертежа. Рекомендую в первую очередь. 2) Изобразить только тело. Годится, когда у тела несложная и очевидная проекция. Так, например, в разобранном примере хватило бы и трёхмерного чертежа. Однако тут есть и минус – по 3D-картинке неудобно определять порядок обхода проекции, и этот способ я бы советовал только людям с хорошим уровнем подготовки. 3) Изобразить только проекцию. Тоже неплохо, но тогда обязательны дополнительные письменные комментарии, чем ограничена
область сверху и снизу. Следующее тело для самостоятельного дела: Пример 33 С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями В данном случае область интегрирования задана преимущественно неравенствами, и это даже лучше – множество
неравенств …Тёмный лес? Вам сюда + сюда либо сюда – поднимаем геометрию! Примерный образец оформления задачи в конце урока. Продолжаем разминаться: Пример 34 Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Выполнить чертёж.
Решение: формулировка «выполнить чертёж» даёт нам некоторую свободу, но, скорее всего, подразумевает выполнение пространственного чертежа. Однако и проекция тоже не помешает, тем более, она здесь не самая простая. Придерживаемся отработанной ранее тактики, сначала разберёмся с поверхностями, параллельными оси аппликат.
Уравнения таких поверхностей не содержат в явном виде переменную «зет»: Но две прямые
Определим порядок обхода тела, при этом «иксовые» и «игрековые» пределы интегрирования удобнее выяснять по
двумерному чертежу: Таким образом: 1) 2) Напоминаю, что при интегрировании по «игрек» – «икс» считается константой, поэтому константу 3) И заключительный, внимательный аккорд: Ответ: Да, чуть не забыл, в большинстве случаев полученный результат малополезно (и даже вредно) сверять с трёхмерным чертежом, поскольку с большой вероятностью возникнет иллюзия объёма, о которой я рассказал в одной из статей сайта. Суть иллюзии состоит в том, что люди склонны неверно оценивать объём «на глазок», мы его либо занижаем, либо завышаем. Так, человек за среднестатистическую жизнь суммарно выпивает жидкости объёмом со стандартную комнату 18 кв. м., что кажется очень малым объёмом. В нашей задаче наоборот – если вы посмотрите на пространственный чертёж, то вам покажется, что тело содержит больше четырёх «кубиков». И после познавательного отступления задание для самостоятельного решения: Пример 35 Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и
его проекции на плоскость
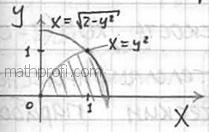
Обратите внимание, что условие этой задачи безвариантно требует выполнения обоих чертежей. Примерный образец оформления в конце книги. Не редкость, когда выполнение трёхмерного чертежа затруднено, и этой ситуации посвящены ближайшие примеры: Пример 36 С помощью тройного интеграла найти объём тела, ограниченного поверхностями Решение: проекция здесь несложная, но вот над порядком её обхода нужно подумать. Если
выбрать 1-й способ, то фигуру придётся разделить на 2 части, что
неиллюзорно грозит вычислением суммы двух тройных интегралов. В этой связи гораздо перспективнее выглядит 2-й путь. Выразим
Теперь дело за телом. Снизу оно ограничено плоскостью Но есть и третий, исконно русский метод решения проблемы – забить =). И вместо трёхмерного чертежа обойтись словесным
описанием: «Данное тело ограничено цилиндрами «Вертикальные» пределы интегрирования, очевидно, таковы: Вычислим объём тела, не забывая, что проекцию мы обошли менее распространённым способом: 1) 2) 3) Ответ: Как вы заметили, предлагаемые в задачах телА часто ограничены плоскостью Легко убедиться, что получится тот же самый результат: Кроме того, «любимая» плоскость может оказаться вообще не при делах, простейший пример: шар, расположенный выше
плоскости Все эти случаи мы рассмотрим, а пока аналогичное задание для самостоятельного решения: Пример 37 С помощью тройного интеграла найти объём тела, ограниченного поверхностями: Сверяемся с решением в конце книги и переходим к параграфу с не менее популярными материалами:
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за пару дней!
Научись решать за пару дней!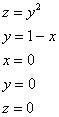
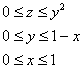
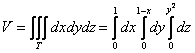
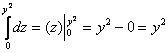
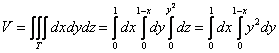
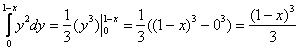
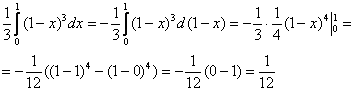
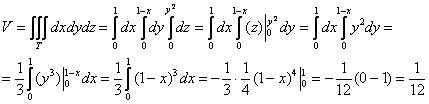
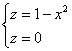
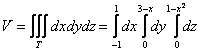
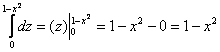
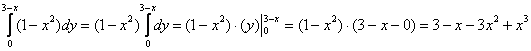
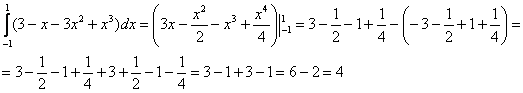
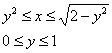
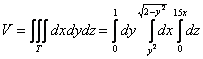
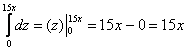
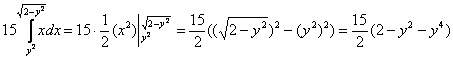
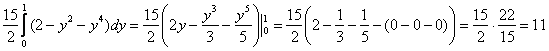
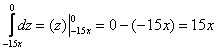
 2.3. Тройной интеграл в цилиндрических координатах
2.3. Тройной интеграл в цилиндрических координатах 2.1. Понятие тройного инетграла
2.1. Понятие тройного инетграла