1.2. Область интегрирования и порядок её обхода
В этом параграфе мы рассмотрим важнейший вопрос – как перейти к повторным интегралам и
правильно расставить пределы интегрирования. Как было сказано выше, сделать это можно так:
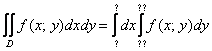 И так: И так: 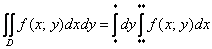
На практике эта вроде бы несложная задача вызывает наибольшие затруднения, и студенты часто путаются в расстановке
пределов интегрирования. Исправим ситуацию:
Пример 1
Дан двойной интеграл 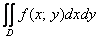 с
областью с
областью 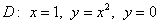 . Перейти к повторным
интегралам и расставить пределы интегрирования двумя способами. . Перейти к повторным
интегралам и расставить пределы интегрирования двумя способами.
Решение: изобразим область интегрирования на чертеже, фигура простейшая:
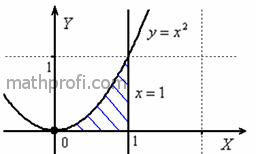
Теперь я выдам вам орудие труда – палку-копалку лазерную указку. Задача состоит в том, чтобы «просканировать» лучом лазера
каждую точку заштрихованной области:
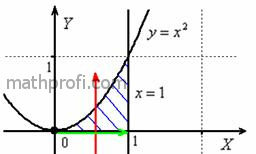
Луч лазера проходит область интегрирования строго снизу вверх, то есть указку вы ВСЕГДА держите
ниже плоской фигуры. Луч входит в область через ось абсцисс, которая задаётся уравнением 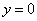 и выходит из области через параболу и выходит из области через параболу 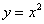 (красная стрелка). Чтобы
просветить всю область, вам нужно строго слева направо провести указкой вдоль оси (красная стрелка). Чтобы
просветить всю область, вам нужно строго слева направо провести указкой вдоль оси 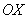 от 0 до 1 (зелёная стрелка). Итак, «игрек»
изменяется от 0 до от 0 до 1 (зелёная стрелка). Итак, «игрек»
изменяется от 0 до 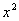 , а «икс»
при этом изменяется от 0 до 1. В задачах сей факт записывают в виде неравенств: , а «икс»
при этом изменяется от 0 до 1. В задачах сей факт записывают в виде неравенств:
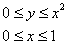
Данные неравенства называют порядком обхода области интегрирования или просто порядком
интегрирования. После того, как мы разобрались с порядком обхода, можно перейти от двойного интеграла к повторным
интегралам:
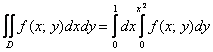
 1.2.1. Как изменить порядок обхода области? 1.2.1. Как изменить порядок обхода области?
 1.1.3. Алгоритм решения двойного интеграла 1.1.3. Алгоритм решения двойного интеграла
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
|

 Научись решать за пару дней!
Научись решать за пару дней!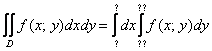 И так:
И так: 

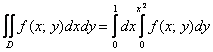
 1.2.1. Как изменить порядок обхода области?
1.2.1. Как изменить порядок обхода области? 1.1.3. Алгоритм решения двойного интеграла
1.1.3. Алгоритм решения двойного интеграла