|
Блиц-курс – Кратные и криволинейные интегралы |
2.5. Тройной интеграл в сферических координатахДо сих пор мы использовали цилиндрическую систему координат, которая, по технической сути, представляет собой «плоскую» полярную систему + дополнительную координату «зет». Но есть задачи, где невероятно удобны сферические координаты. В данной системе координат точка Где используется сферическая система координат? Ну, конечно, в астрономии. Однако своё скромное применения она нашла и при вычислении тройных интегралов: Пример 48 Вычислить интеграл Решение: тот редкий случай, когда можно обойтись без чертежа. Однако я всё же втайне мечтаю, что потомки
оценят художественную ценность моих сканов:) Определим порядок обхода тела. Для этого нужно найти уравнение сферы Теперь смотрИте на чертёж выше и представляйте это в динамике: – луч радара исходит из начала координат и выходит из тела через сферу В результате мы учли все точки шара, т.е. полностью обошли тело интегрирования. Преобразуем подынтегральную функцию Остальное дело техники: Ответ: Этот тройной интеграл можно было взять и через цилиндрические координаты, но вычисления получились бы заметно труднее. Когда целесообразно использовать сферическую систему координат? Прежде всего, когда нет проблем с определением зенитного угла. Как правило, это шар и его части, шар, вложенный в другой шар и т.п. конструкции. Кстати, шаровой сектор из Примера 46 – там этот угол прям конфетка, и я предлагаю вам самостоятельно решить данный интеграл вторым способом: Пример 49 Вычислить тройной интеграл Ответы, разумеется, должны совпасть. Следует однако заметить, что само по себе использование сферических координат ещё не означает, что решение получится проще. Но самое интересное только начинается:
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за пару дней!
Научись решать за пару дней!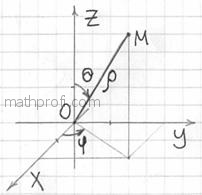 Угол
Угол 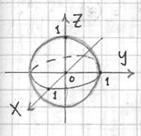 Тройной интеграл
вычислим с помощью сферической системы координат. Формулы перехода к ней таковы:
Тройной интеграл
вычислим с помощью сферической системы координат. Формулы перехода к ней таковы: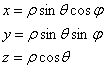
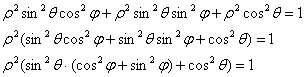
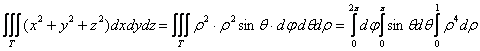
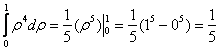
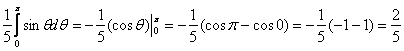
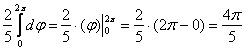
 2.6. Физические приложения тройного интеграла
2.6. Физические приложения тройного интеграла 2.4. Как вычислить произвольный тройной интеграл?
2.4. Как вычислить произвольный тройной интеграл?