1.4. Как вычислить произвольный двойной интеграл?
Только что был рассмотрен элементарный случай, когда подынтегральная
функция 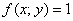 , и сейчас мы
начнём «набивать» наш двойной интеграл , и сейчас мы
начнём «набивать» наш двойной интеграл 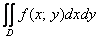 более разнообразной «начинкой». И у таких интегралов тоже есть
свой геометрический смысл! Пусть функция более разнообразной «начинкой». И у таких интегралов тоже есть
свой геометрический смысл! Пусть функция 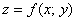 существует в каждой точке существует в каждой точке 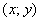 плоской области плоской области 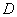 (см. рис).
Геометрически она задаёт некоторую поверхность в трёхмерном
пространстве. Для определенности считаем, что (см. рис).
Геометрически она задаёт некоторую поверхность в трёхмерном
пространстве. Для определенности считаем, что 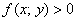 , то есть поверхность полностью (это важно!)
расположена над плоскостью , то есть поверхность полностью (это важно!)
расположена над плоскостью 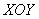 . Тогда соответствующий двойной интеграл численно равен
объёму цилиндрического бруса . Тогда соответствующий двойной интеграл численно равен
объёму цилиндрического бруса 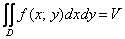 : :
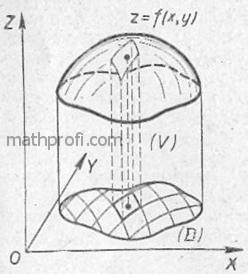 Что такое
цилиндрический брус, думаю, всем понятно из чертежа, который я отсканировал из старого-старого советского учебника.
Тем не менее, закомментирую. Что такое
цилиндрический брус, думаю, всем понятно из чертежа, который я отсканировал из старого-старого советского учебника.
Тем не менее, закомментирую.
Плоская фигура 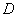 (заштрихована на чертеже) полностью лежит в плоскости (заштрихована на чертеже) полностью лежит в плоскости 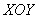 и брус ограничен
областью и брус ограничен
областью 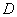 снизу. Сверху брус
как раз ограничен поверхностью снизу. Сверху брус
как раз ограничен поверхностью 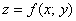 , которая представляет собой такую «шапку». Плоская область , которая представляет собой такую «шапку». Плоская область 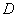 по своей границе
перпендикулярными лучами
вырезает из поверхности по своей границе
перпендикулярными лучами
вырезает из поверхности 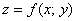 эту шапочку. И сбоку брус, очевидно,
ограничен этими лучами. На пунктирные линии внутри и «заплатки» с точками не обращайте внимания, они нужны для подробного
изложения теории. Я не стал тереть их в графическом редакторе – вдруг кого заинтересует J. эту шапочку. И сбоку брус, очевидно,
ограничен этими лучами. На пунктирные линии внутри и «заплатки» с точками не обращайте внимания, они нужны для подробного
изложения теории. Я не стал тереть их в графическом редакторе – вдруг кого заинтересует J.
В большинстве практических задач двойной интеграл нужно вычислить лишь формально, но для лучшего
понимания мы будем неоднократно привлекать смысл:
Пример 13
Вычислить двойной интеграл 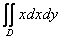 , , 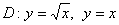 . Изменить порядок интегрирования и вычислить двойной интеграл
вторым способом. . Изменить порядок интегрирования и вычислить двойной интеграл
вторым способом.
Решение: изобразим область интегрирования 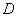 на чертеже: на чертеже:
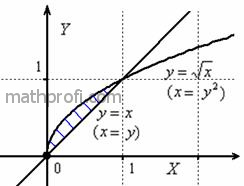
Напоминаю, что выполнение чертежа – строго показанный начальный этап решения. За исключением каких-то
совсем простых случаев. Они, кстати, тоже будут.
При этом чертёж крайне важно выполнить правильно и точно, поскольку ошибка в графике незамедлительно «запорет» всё
задание. …О как стращать вас начал J.
Выберем первый, «традиционный» порядок обхода:
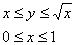
Таким образом: 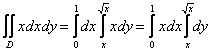 . .
И обратите внимание на следующее действие: здесь можно вынести «икс» из внутреннего интеграла во внешний
интеграл. Почему? Во внутреннем интеграле 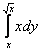 интегрирование проводится по «игрек», следовательно,
«икс» считается константой. А любую константу можно вынести за знак интеграла, что благополучно и сделано. интегрирование проводится по «игрек», следовательно,
«икс» считается константой. А любую константу можно вынести за знак интеграла, что благополучно и сделано.
С интегралами в который раз и настоятельно рекомендую разбираться по пунктам:
1) Используя формулу Ньютона-Лейбница, найдём внутренний интеграл:
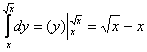 –
вместо «игрека» подставляем функции! –
вместо «игрека» подставляем функции!
2) Результат, полученный в первом пункте, подставим во внешний интеграл 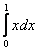 , при этом ни в коем случае не забываем про
«икс», который там уже находится: , при этом ни в коем случае не забываем про
«икс», который там уже находится:
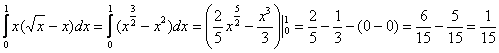
Выполним вторую часть задания, а именно изменим порядок обхода области и
вычислим двойной интеграл вторым способом. Перейдём к обратным функциям:
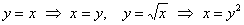 и второй порядок обхода: и второй порядок обхода:
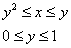
Таким образом: 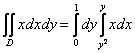 – а вот
здесь уже «икс» является «родным» для внутреннего интеграла, поэтому его нельзя вынести во внешний
интеграл. – а вот
здесь уже «икс» является «родным» для внутреннего интеграла, поэтому его нельзя вынести во внешний
интеграл.
1) Используя формулу Ньютона-Лейбница, вычислим внутренний интеграл:
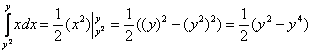 – ВМЕСТО «икса»
подставляются функции (пределы интегрирования)! – ВМЕСТО «икса»
подставляются функции (пределы интегрирования)!
2) Результат, полученный в первом пункте, подставим во внешний интеграл и проведём окончательные вычисления:
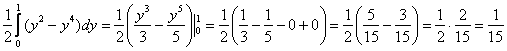
Результаты совпали, значит, задание выполнено верно, ответ: 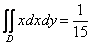
Дополнительно поясню геометрический смысл разобранного примера. В нём мы рассмотрели двойной интеграл 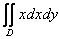 со следующей областью со следующей областью 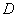 : :
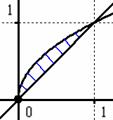 Подынтегральная функция Подынтегральная функция 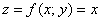 задаёт плоскость в пространстве, которая расположена над
областью задаёт плоскость в пространстве, которая расположена над
областью 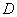
Теперь из начала координат перпендикулярно экрану монитора мысленно проведите себе в лоб стрелку оси 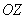 . Точно так же из границы области . Точно так же из границы области 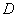 направьте на себя
перпендикулярные лучи. Эти лучи вырежут кусочек из плоскости направьте на себя
перпендикулярные лучи. Эти лучи вырежут кусочек из плоскости 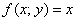 . …Все представили полученный цилиндрический брус? Снизу он
ограничен заштрихованной областью, сверху – кусочком плоскости и сбоку – лучами. . …Все представили полученный цилиндрический брус? Снизу он
ограничен заштрихованной областью, сверху – кусочком плоскости и сбоку – лучами.
Полученный в задаче результат 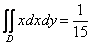 численно равен объёму этого бруса. Такой вот маленький
брусочек. Впрочем, «маленький» – понятие относительное J. численно равен объёму этого бруса. Такой вот маленький
брусочек. Впрочем, «маленький» – понятие относительное J.
Если двойной интеграл получился положительным, это означает, что соответствующее пространственное тело
(«брус») полностью или бОльшей (по объёму) частью лежит над областью 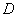 (выше плоскости (выше плоскости 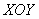 ). Следует заметить, что частный случай ). Следует заметить, что частный случай 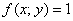 интерпретируется не только как площадь области интерпретируется не только как площадь области 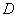 , но и как объём соотвествующего бруса единичной высоты. , но и как объём соотвествующего бруса единичной высоты.
Двойной интеграл может быть отрицательным, в таких случаях график функции 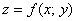 полностью (или бОльшей частью) лежит
под областью полностью (или бОльшей частью) лежит
под областью 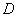 . Это тоже объем тела, только со знаком минус, поскольку
поверхность полностью (или бОльшей частью) лежит под координатной плоскостью . Это тоже объем тела, только со знаком минус, поскольку
поверхность полностью (или бОльшей частью) лежит под координатной плоскостью 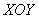 . .
И особый случай, нулевой: 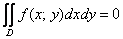 . Такое бывает, когда область . Такое бывает, когда область 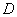 представляет собой линию на плоскости или даже точку.
Или же часть бруса лежит над областью представляет собой линию на плоскости или даже точку.
Или же часть бруса лежит над областью 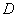 (не ниже плоскости (не ниже плоскости 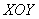 ) и такая же по объёму часть – под
областью (не выше ) и такая же по объёму часть – под
областью (не выше 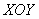 ). В этом случае объёмы формально взаимоуничтожают друг
друга. ). В этом случае объёмы формально взаимоуничтожают друг
друга.
Задание для самостоятельного решения.
Пример 14
Вычислить двойной интеграл  , , 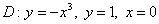 Выполнить проверку, изменив порядок интегрирования и вычислив двойной интеграл 2-м способом. Выполнить проверку, изменив порядок интегрирования и вычислив двойной интеграл 2-м способом.
Если есть время, старайтесь всегда выполнять такую проверку,
даже если этого не требуется в условии
Вычислили интеграл одним способом – затем изменили порядок обхода области и вычислили вторым способом.
Очень хорошо, если у вас под рукой есть калькулятор, на котором можно считать обыкновенные дроби, он значительно ускорит
вычисления. А если нет, ничего страшного, к настоящему курсу я приложил фирменный и улучшенный «дробовик» проекта. Примерный образец чистового оформления примера в конце книги.
Продолжаем совершенствовать технику вычислений:
Пример 15
Вычислить двойной интеграл
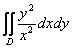 , , 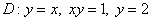
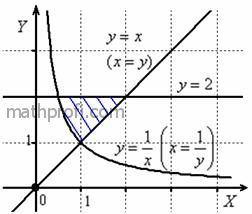 Решение: изобразим область интегрирования на чертеже: Решение: изобразим область интегрирования на чертеже:
После того, как корректно выполнен чертеж и правильно (!) определена область
интегрирования, самое время разобраться с порядком обхода.
Согласно первому способу, область придётся разделить на две части, при этом необходимо будет вычислить следующие
интегралы:
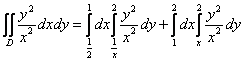
Приятного, так скажем, мало. Проанализируем, а не проще ли использовать второй способ обхода области? Перейдем к обратным
функциям, переход здесь элементарен:
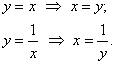
Таким образом, порядок обхода области:
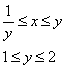
и соответствующие повторные интегралы:
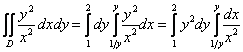 – ну вот, совсем другое
дело. – ну вот, совсем другое
дело.
И снова заметьте, что во внутреннем интеграле интегрирование осуществляется по «икс», поэтому константу 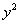 можно сразу вынести во внешний интеграл можно сразу вынести во внешний интеграл
1) Найдём внутренний интеграл:
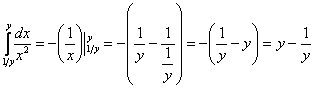
Всё-таки подстановка пределов интегрирования, порой, выглядит своеобразно. Сначала ВМЕСТО «икса» мы подставили верхний
предел интегрирования 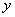 , затем
ВМЕСТО «икса» подставили нижний предел интегрирования , затем
ВМЕСТО «икса» подставили нижний предел интегрирования 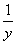 . Будьте внимательны при подстановках! И на всякий пожарный –
действия с многоэтажными дробями. . Будьте внимательны при подстановках! И на всякий пожарный –
действия с многоэтажными дробями.
2) Результат предыдущего пункта подставим во внешний интеграл, при этом не забываем про 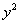 , который там уже находится: , который там уже находится:
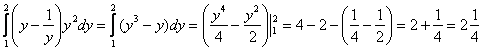
Ответ: 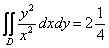
Для тренировки можете попробовать вычислить интеграл менее рациональным способом: 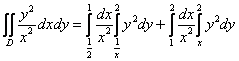 . Результаты должны совпасть. . Результаты должны совпасть.
Пример 16
Вычислить двойной интеграл 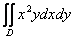 , , 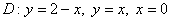
Самостоятельно постройте область 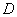 и проанализируйте, какой способ обхода области выгоднее
использовать. Полное решение и ответ в конце книги. и проанализируйте, какой способ обхода области выгоднее
использовать. Полное решение и ответ в конце книги.
Усложняем задачу, теперь подынтегральная функция будет представлять собой сумму. Рассмотрим еще два примера, где я
остановлюсь на приёме вычисления интеграла, который типичен и эффективен для кратных интегралов:
Пример 17
Вычислить двойной интеграл
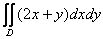 , , 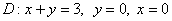
И сразу отметим то, чего делать не нужно – в данном случае не следует
использовать свойство линейности кратного интеграла и представлять его в виде:
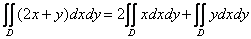 …Почему? Вычислений
заметно прибавится! …Почему? Вычислений
заметно прибавится!
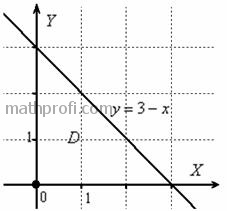 Решение: область Решение: область 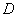 незамысловата, даже штриховать не буду: незамысловата, даже штриховать не буду:
В данном примере, как легко заметить, порядок интегрирования не имеет особого значения, поэтому выберем первый, более
привычный вариант обхода области:
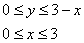
Таким образом:
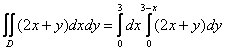 , и здесь, в отличие
от двух предыдущих примеров, из внутреннего интеграла ничего вынести нельзя, поскольку начинкой является
сумма. , и здесь, в отличие
от двух предыдущих примеров, из внутреннего интеграла ничего вынести нельзя, поскольку начинкой является
сумма.
С повторными интегралами опять разбираемся по отдельности:
1) Сначала берём внутренний интеграл:
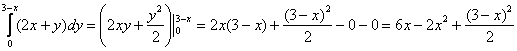
И тут речь зашла о частном интегрировании: если интегрирование проводится по «игрек», то переменная «икс»
считается константой. И наоборот.
Перед использованием формулы Ньютона-Лейбница строго рекомендована проверка, найдём частную производную по «игрек»:
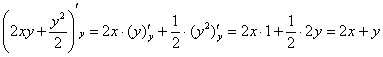 – в результате получена
исходная подынтегральная функция, значит, всё в порядке. – в результате получена
исходная подынтегральная функция, значит, всё в порядке.
И только после этого подставляем пределы интегрирования – сначала ВМЕСТО «игреков» мы подставили 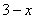 , а затем – нижний предел
(нули). После подстановки должны остаться только «иксы». , а затем – нижний предел
(нули). После подстановки должны остаться только «иксы».
И, наконец, такой вопрос – почему я оставил результат в виде 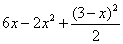 ? ?
Ведь можно раскрыть скобки и привести подобные слагаемые! В данном случае это сделать несложно, и «чайникам», вероятно,
лучше так и поступить. Но если будет не вторая, а 3-я или 4-я степень? На самом деле линейную функцию в степени
выгоднее проинтегрировать, не раскрывая скобок! Данный приём я уже применял и подробно комментировал в теме
Определённые интегралы при нахождении объёма тела
вращения.
Ещё раз посмотрим, как он работает:
2) Берём оставшийся внешний интеграл:

При нахождении интеграла 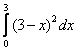 использован метод подведения функции под знак дифференциала. Перед
подстановкой пределов интегрирования для проверки берём «обычные» производные использован метод подведения функции под знак дифференциала. Перед
подстановкой пределов интегрирования для проверки берём «обычные» производные 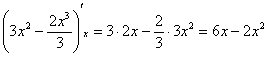 и: и:
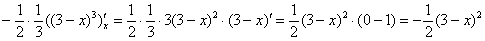
Ответ: 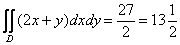
Пример 18
Вычислить двойной интеграл 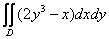 , , 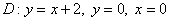
Это пример для самостоятельного решения. В образце, как и в разобранном примере выше, использован первый способ обхода
области. Но это ещё далеко и далеко не всё. Не пропускаем (!) нижеследующие задачи ;)
Пример 19
Вычислить двойной интеграл 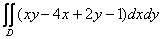 , , 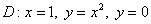
Решение: область интегрирования тут простая, и основной гемор ожидается как раз в вычислениях:
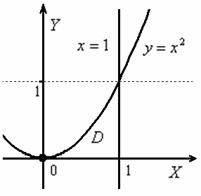
Выберем привычный порядок обхода области:
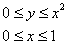
Таким образом:
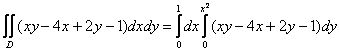 С интегралами
разделаемся по отдельности: С интегралами
разделаемся по отдельности:
1) Интегрируем внутренний интеграл по «игрек» («икс» считается константой):
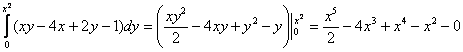
Перед подстановкой пределов интегрирования обязательно выполняем проверку, а именно берём частную производную по
«игрек»:
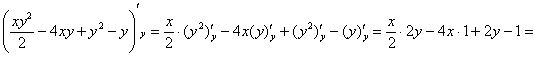
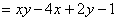 – в результате
получена исходная подынтегральная функция, ОК. – в результате
получена исходная подынтегральная функция, ОК.
Далее. Будьте ПРЕДЕЛЬНО внимательны в подстановке пределов интегрирования: сначала ВМЕСТО «игреков» подставляем
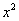 , затем – ноль. При
оформлении решения вполне допустимо записать один, а не несколько нолей, как это сделано в этом примере. После интегрирования
по «игрек» и подстановок должны остаться только «иксы»! , затем – ноль. При
оформлении решения вполне допустимо записать один, а не несколько нолей, как это сделано в этом примере. После интегрирования
по «игрек» и подстановок должны остаться только «иксы»!
2) Подставляем «иксовый трофей» во внешний интеграл:
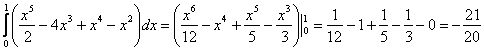 ,
готово. ,
готово.
Да, не забываем о промежуточной проверке:
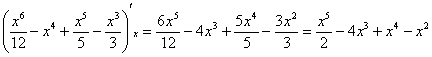 , ОК. , ОК.
Теперь решим задачу вторым способом, тут есть о чём поговорить. Перейдём к обратной функции 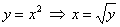 и изменим порядок обхода области: и изменим порядок обхода области:
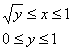
Таким образом:
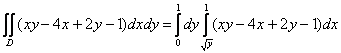
1) Интегрируя по «икс» («игрек» – константа), вычислим внутренний интеграл:
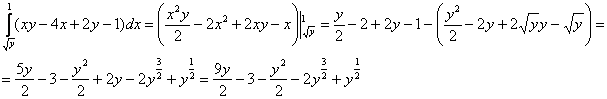
Обязательная промежуточная проверка, берём частную производную по «икс»:
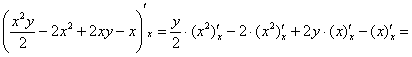
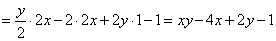 – получена
подынтегральная функция. – получена
подынтегральная функция.
Подстановка пределов интегрирования здесь сложнее: сначала вместо «иксов» подставляем 1, затем
вместо «иксов» подставляем 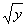 . После интегрирования по «икс» и подстановок пределов интегрирования
должны остаться только «игреки». Степени рекомендую оставить в виде . После интегрирования по «икс» и подстановок пределов интегрирования
должны остаться только «игреки». Степени рекомендую оставить в виде 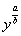 , а не преобразовывать их в корни – будет
удобнее интегрировать на втором шаге: , а не преобразовывать их в корни – будет
удобнее интегрировать на втором шаге:
2) Подставляем «игрековый трофей» во внутренний интеграл и интегрируем по 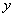 : :
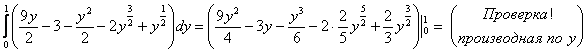 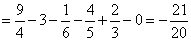 – результаты совпали, как оно и должно
быть. Легко заметить, что первый способ решения был заметно проще. – результаты совпали, как оно и должно
быть. Легко заметить, что первый способ решения был заметно проще.
Всегда перед решением анализируйте – какой путь легче и короче
Ответ: 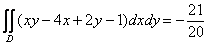
Результат получился отрицательным. Геометрически это обозначает, что график подынтегральной функции 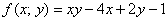 (поверхность в пространстве) полностью
или бОльшей частью (не проверял) располагается ниже области интегрирования (поверхность в пространстве) полностью
или бОльшей частью (не проверял) располагается ниже области интегрирования 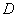 под плоскостью под плоскостью 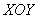 . .
Другой технический момент касается дробей. Дроби в рассмотренном примере еще худо-бедно можно привести к общему знаменателю
вручную. Но не удивляйтесь, если на практике получится ответ вроде 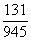 , по крайне мере, в своей коллекции я нашел немало диких
примеров, где без калькулятора-«дробовика» фактически не обойтись. Ещё раз напоминаю, что он приложен к этой книге. , по крайне мере, в своей коллекции я нашел немало диких
примеров, где без калькулятора-«дробовика» фактически не обойтись. Ещё раз напоминаю, что он приложен к этой книге.
Пример 20
Вычислить двойной интеграл по области 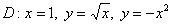
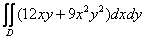
Решаем и ни в коем случае не останавливаемся:
Пример 21
Вычислить двойной интеграл по области 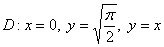
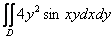
Решение: в ходе выполнения чертежа может возникнуть трудность с построением прямой 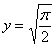 , которая параллельна оси , которая параллельна оси 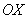 . Ничего сложного: если . Ничего сложного: если 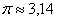 , то , то 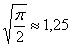 – примерно на этом уровне и следует провести
прямую: – примерно на этом уровне и следует провести
прямую:
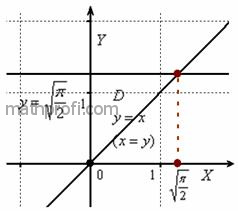
После выполнения чертежа нужно выяснить, какой порядок обхода области
выгоднее применить.
Рассмотрим первый способ обхода:
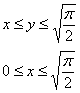
Тогда: 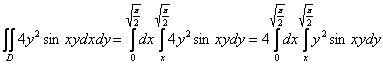
Очевидно, что первый способ является крайне неудачным, поскольку внутренний интеграл  придётся дважды брать по частям. придётся дважды брать по частям.
Но есть альтернатива!
Выберем второй способ обхода области:
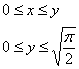
Следовательно: 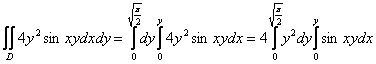
Выглядит гораздо привлекательнее, начинаем вычисления:
1) По формуле Ньютона-Лейбница разберёмся с внутренним интегралом:
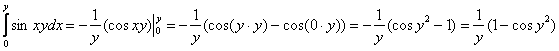
Когда мы интегрируем по «икс», переменная «игрек» считается константой. Если возникают трудности с
интегрированием, можно прибегнуть даже к такому способу: на черновике временно замените «игрек» конкретным числом, например,
«пятёркой»:
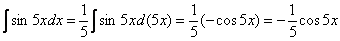 . .
Теперь замените «пятёрку» обратно – «игреком»: 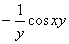
И, конечно же, проверка дифференцированием по «икс»:
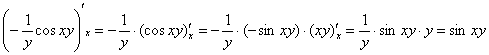
Далее при подстановке пределов интегрирования сначала вместо «икса» подставляем 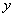 , затем – ноль. После подстановки должны
остаться только «игреки». , затем – ноль. После подстановки должны
остаться только «игреки».
2) Полученный результат 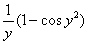 перемещаем во внешний интеграл, не забывая, что там уже
есть перемещаем во внешний интеграл, не забывая, что там уже
есть 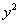 и константа 4,
после чего интегрируем «по игрек» и константа 4,
после чего интегрируем «по игрек»
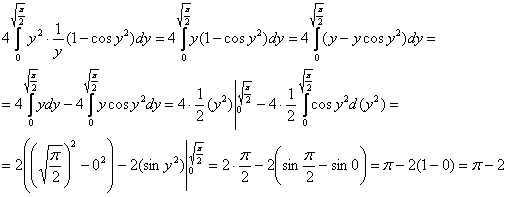
Второй интеграл взят методом подведения функции под знак
дифференциала.
Ответ: 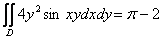
Таким образом, выбор порядка обхода иногда зависит не только от самой области интегрирования, но и от
подынтегральной функции.
Пример 22
Вычислить двойной интеграл 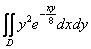 по области по области 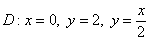
Решаем самостоятельно. …А теперь признАйтесь, вам так же хорошо, как мне? :) Это мудрое пожелание я всегда высказываю своим
ученикам, но они почему-то смеются – хорошо должно быть каждый день! И даже если всё не очень, то к этому состоянию духа нужно
непременно стремиться. Изучим ещё один важный метод решения:
 1.5. Как вычислить двойной интеграл в полярных координатах? 1.5. Как вычислить двойной интеграл в полярных координатах?
 1.3. Как найти площадь фигуры с помощью двойного интеграла? 1.3. Как найти площадь фигуры с помощью двойного интеграла?
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
|

 Научись решать за пару дней!
Научись решать за пару дней! Что такое
цилиндрический брус, думаю, всем понятно из чертежа, который я отсканировал из старого-старого советского учебника.
Тем не менее, закомментирую.
Что такое
цилиндрический брус, думаю, всем понятно из чертежа, который я отсканировал из старого-старого советского учебника.
Тем не менее, закомментирую.
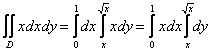 .
.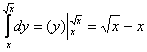 –
вместо «игрека» подставляем функции!
–
вместо «игрека» подставляем функции!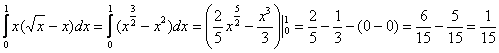
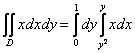 – а вот
здесь уже «икс» является «родным» для внутреннего интеграла, поэтому его нельзя вынести во внешний
интеграл.
– а вот
здесь уже «икс» является «родным» для внутреннего интеграла, поэтому его нельзя вынести во внешний
интеграл.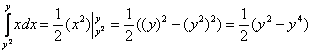 – ВМЕСТО «икса»
подставляются функции (пределы интегрирования)!
– ВМЕСТО «икса»
подставляются функции (пределы интегрирования)!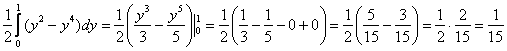
 Подынтегральная функция
Подынтегральная функция  Решение: изобразим область интегрирования на чертеже:
Решение: изобразим область интегрирования на чертеже: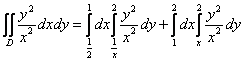
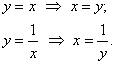
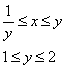
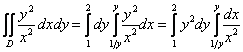 – ну вот, совсем другое
дело.
– ну вот, совсем другое
дело.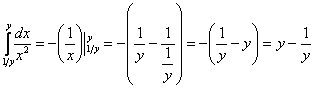
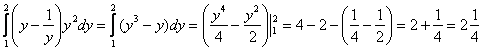
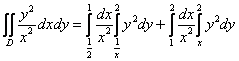 . Результаты должны совпасть.
. Результаты должны совпасть. Решение: область
Решение: область 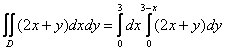 , и здесь, в отличие
от двух предыдущих примеров, из внутреннего интеграла ничего вынести нельзя, поскольку начинкой является
сумма.
, и здесь, в отличие
от двух предыдущих примеров, из внутреннего интеграла ничего вынести нельзя, поскольку начинкой является
сумма.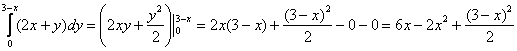
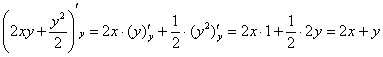 – в результате получена
исходная подынтегральная функция, значит, всё в порядке.
– в результате получена
исходная подынтегральная функция, значит, всё в порядке.
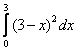 использован
использован 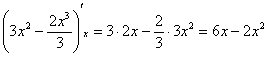 и:
и:
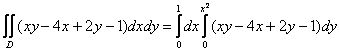 С интегралами
разделаемся по отдельности:
С интегралами
разделаемся по отдельности: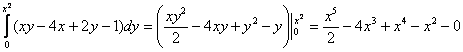
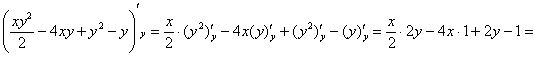
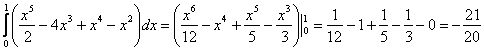 ,
готово.
,
готово.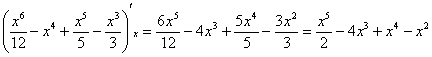 , ОК.
, ОК.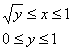
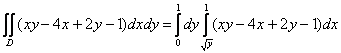
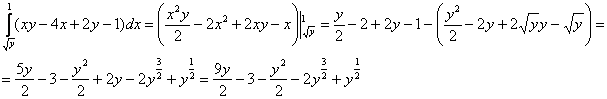
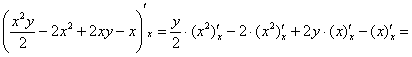
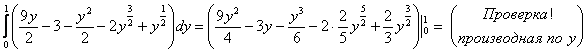

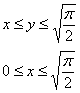
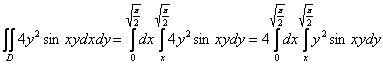
 придётся дважды
придётся дважды 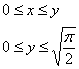
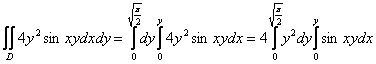
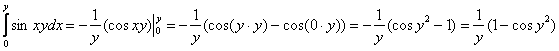
 1.5. Как вычислить двойной интеграл в полярных координатах?
1.5. Как вычислить двойной интеграл в полярных координатах? 1.3. Как найти площадь фигуры с помощью двойного интеграла?
1.3. Как найти площадь фигуры с помощью двойного интеграла?