|
Блиц-курс – Кратные и криволинейные интегралы |
1.5. Как вычислить двойной интеграл в полярных координатах?Типовое задание формулируется примерно так: «Вычислить двойной интеграл, используя полярную систему координат». После чего для решения
предлагается… обычный двойной интеграл Пример 23 Вычислить площадь плоской фигуры, ограниченную линиями На первом этапе решения ничего нового. Выполняем чертёж области Площадь фигуры стандартно рассчитывается по формуле То есть, от интегрирования по декартовым «иксу» и «игреку» мы перешли к интегрированию по полярному радиусу «эр» и
полярному углу «фи». Обратите внимание на появившийся множитель Таким образом: Сведём двойной интеграл И здесь я вновь рекомендую оформлять решение в два пункта: 1) Сначала возьмём внутренний интеграл: 2) Подставляем трофей во внешний интеграл и используем популярную формулу понижения степени Ответ: В простых случаях, как этот, вычисления можно оформить и «одной строкой»: К слову, совсем забыл привести такое решение для случая декартовых координат, решим «быстрым» способом, скажем, простенький
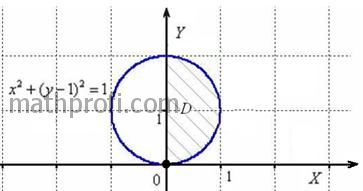
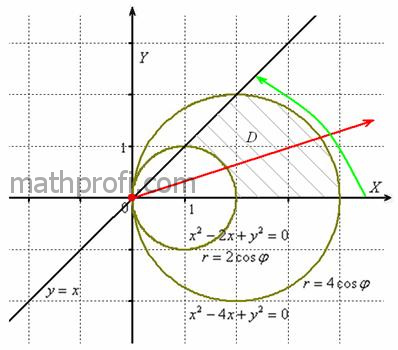
Пример 13: Но злоупотреблять короткой дорожкой не советую – повышается риск запутаться. В разобранной задаче жёстко требовалось использовать полярную систему координат, и это очень хорошо! Я не иронизирую. Как ни странно, более свободная формулировка условия может здОрово осложнить жизнь. Отрубим ящерице хвост: «Вычислить площадь плоской фигуры, ограниченную линиями Дело в том, что площадь данной фигуры рассчитывается и с помощью двойного интеграла Давайте ещё укоротим условие: «Вычислить площадь плоской фигуры, ограниченную линиями Здесь появилась новая степень свободы, и площадь фигуры помимо прочих способов можно рассчитать с помощью однократного интеграла (решение будет почти совпадать с решением через двойной интеграл). Впрочем, рецензент может не оценить такую вольность :). Чуть позже я коснусь ещё одной важной разновидности условия, а пока рассмотрим более содержательный пример: Пример 24 С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями Решение: изобразим данную фигуру на чертеже. С прямыми
Таким образом: Итак, площадь фигуры вычислим с помощью двойного интеграла, используя полярную систему координат:
По формулам перехода
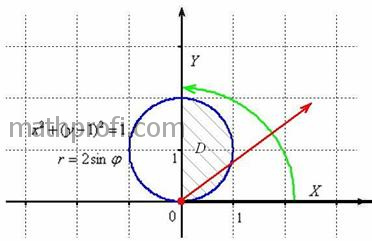
Теперь выясним порядок обхода области. Луч радара (см. рис. выше) входит в область через окружность Напомню также, что «альфа» и «бета» – это не просто формальные значения углов: полярное уравнение И после такой шикарной справки возвращаемся к решению. По результатам «сканирования» области мы выяснили, что на промежутке
Перейдём к повторным интегралам: 1) Раскрутим внутренний интеграл: Ответ: Прикинув по чертежу количество клеточек, приходим к выводу, что полученный результат вполне и вполне правдоподобен. Теперь ответим на следующий важный вопрос: Каковы предпосылки для перехода к полярным координатам? Основной предпосылкой является наличие окружности (ей). Подчёркиваю, что это лишь предпосылка, а не обязательное правило! То есть, область интегрирования может быть ограничена окружностью (ями), но переход к полярным координатам только усложнит решение, а то и вообще заведёт его в тупик. Поэтому другим важным условием является удачное «сканирование» области «радаром». Впрочем, в каждом случае нужно смотреть индивидуально. Следующие два примера для самостоятельного решения: Пример 25 С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями Пример 26 Вычислить двойной интеграл, используя полярные координаты И в Примере 26 мы встретили ещё одну распространённую формулировку условия, в которой предложено непосредственно
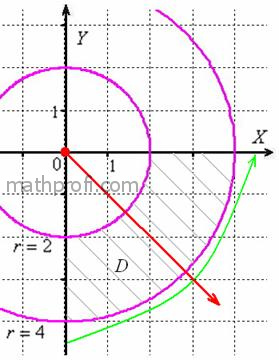
вычислить двойной интеграл. Да, он численно равен площади области Разумеется, в двойном интеграле Пример 27 Вычислить двойной интеграл, используя полярные координаты Решение: область интегрирования здесь очень простая – это часть кольца между концентрическими
окружностями Найдём уравнения окружностей в полярных координатах: Выполним чертёж: Можно было взять промежуток
После подстановки полученное выражение максимально упрощают, но здесь этого особо не потребовалось. Таким образом: 1) Вычислим незамысловатый внутренний интеграл: 2) И внешний, сразу вынося полученную выше константу за пределы интеграла: Ответ: Повторим геометрический смысл полученного результата. Так как Аналогичный пример для самостоятельного решения: Пример 28 Вычислить двойной интеграл, используя полярные координаты Примерный образец чистового оформления задания в конце книги. В соответствующей статье
сайта я также разбираю более редкие интегралы, где можно обойтись даже без чертежа, но это уже углублённый курс.
Напомню заодно, что если условие задачи того не требует – то чертёж можно и не выполнять. Правда, область интегрирования всё
равно придётся представить мысленно. Но даже если у вас есть такие способности, то демонстрировать их совсем не обязательно,
ибо что тяжелА жизнь вундеркинда ;) Исключение составляют какие-то совсем простые области
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2025, Высшая математика – просто и доступно! |

 Научись решать за пару дней!
Научись решать за пару дней!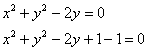
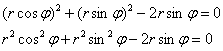
 Когда луч
радара поворачивается от полярной оси
Когда луч
радара поворачивается от полярной оси 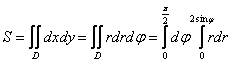 – множитель
– множитель
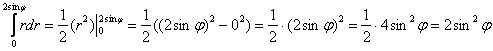
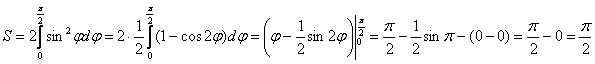 что и
требовалось получить (вспоминаем вычисления по школьной формуле).
что и
требовалось получить (вспоминаем вычисления по школьной формуле).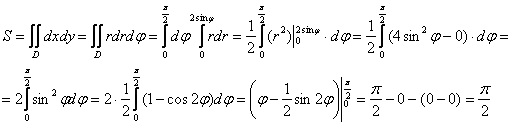

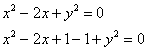
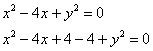
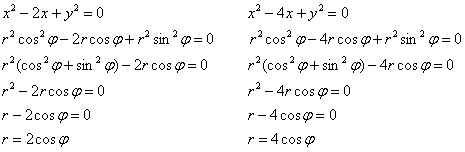
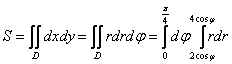
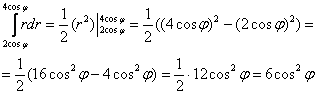

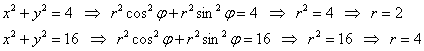
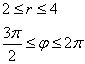
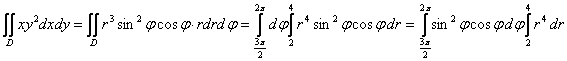
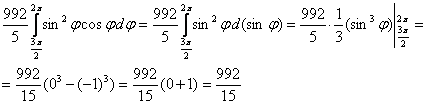
 1.6. Центр тяжести плоской фигуры
1.6. Центр тяжести плоской фигуры 1.4. Как вычислить произвольный двойной интеграл?
1.4. Как вычислить произвольный двойной интеграл?