|
Блиц-курс – Кратные и криволинейные интегралы |
3.3.1. Как вычислить криволинейный интеграл второго рода?Криволинейный интеграл второго рода (начало задачи там) тоже сводится к определённому интегралу, и в результате этого перехода мы должны «избавиться» либо от всех «игреков», либо от всех «иксов». Способ первый, традиционный, где осуществляется переход к интегрированию по переменной Берём уравнение линии После чего подставляем Ответ: Если проинтегрировать наоборот – от точки Второй способ решения состоит в переходе к интегрированию по переменной Чтобы перейти к определённому интегралу, в подынтегральное выражение нужно подставить
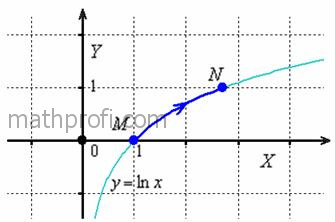
Второй способ оказался технически труднее, но, разумеется, бывает и наоборот. Поэтому перед решением всегда полезно «прикинуть» оба пути*. И да – проверка же, не ленИтесь! * Но тут есть исключение: если фрагмент или весь путь интегрирования параллелен координатной оси, то способ остаётся только один! Ибо проекция этого участка на другую ось равна нулю. Ответ: Для самостоятельного решения я всегда стараюсь подбирать интересные случаи;) Пример 57 Вычислить криволинейный интеграл Прорешиваем и продолжаем нарабатывать технические навыки: Пример 58 Вычислить криволинейный интеграл Решение: для удобства выполним чертёж, не забывая подметить, что линия интегрирования не может пересекать
ось ординат (т.к. 1) Вычислим Результат, кстати, не помешает проверить интегрированием по «игрек». Для этого найдём обратную функцию
Со второй частью всё проще: 2) Контроль по «игрек»: Осталось просуммировать полученные в пунктах 1) и 2) значения: Ответ: Разделение интеграла особенно удобно в тех случаях, когда подынтегральное выражение сильно «наворочено. Очередная «бомба» для самостоятельного решения: Пример 59 Проверить, существует ли интеграл по данной кривой, и вычислить его, если это возможно: Решение и ответ в конце книги.
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за пару дней!
Научись решать за пару дней!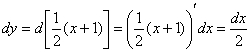
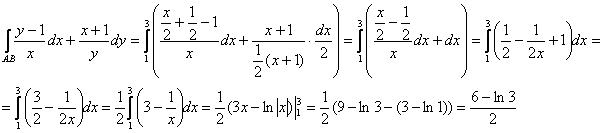
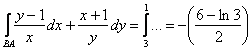 – и здесь легко усмотреть известное свойство
– и здесь легко усмотреть известное свойство 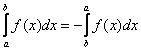 определённого интеграла.
определённого интеграла.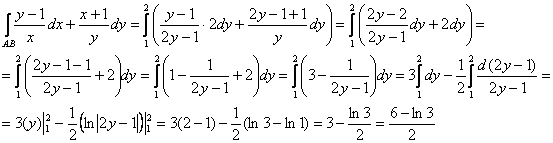
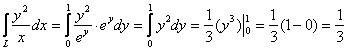 , что и требовалось проверить. Напоминаю,
что второй путь можно смело выбирать и за основной.
, что и требовалось проверить. Напоминаю,
что второй путь можно смело выбирать и за основной.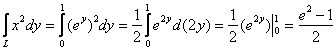
 3.3.2. Если линия задана параметрически
3.3.2. Если линия задана параметрически 3.3. Криволинейные интегралы второго рода
3.3. Криволинейные интегралы второго рода