1.3. Как найти площадь плоской фигуры
с помощью двойного интеграла?
Двойной интеграл 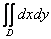 численно
равен площади плоской фигуры численно
равен площади плоской фигуры 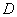 (области интегрирования). Сначала рассмотрим задачу в общем
виде. (области интегрирования). Сначала рассмотрим задачу в общем
виде.
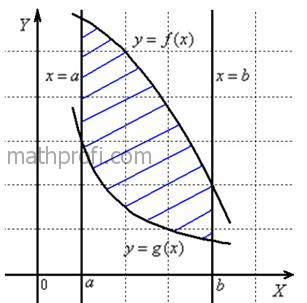
А именно вычислим площадь фигуры 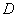 , ограниченной линиями , ограниченной линиями 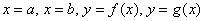 . Для определённости считаем, что . Для определённости считаем, что 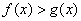 на отрезке на отрезке 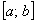 . .
Площадь заштрихованной фигуры численно равна 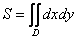 , и сейчас мы «раскрутим» тему. , и сейчас мы «раскрутим» тему.
Выберем первый способ обхода области:
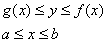
Таким образом: 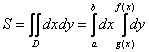
И сразу важный технический приём: повторные интегралы можно считать по отдельности. Сначала внутренний
интеграл, затем – внешний интеграл. Данный способ настоятельно рекомендую «чайникам», да и не только им. Потому что это
удобно.
1) Вычислим внутренний интеграл, при этом интегрирование проводится по переменной «игрек»:
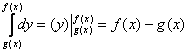
Неопределённый интеграл тут простейший, и далее используется банальная формула Ньютона-Лейбница, с той лишь
разницей, что пределами интегрирования являются не числа, а функции. Сначала подставили в «игрек» (первообразную
функцию) верхний предел, затем – нижний предел
2) Результат первого пункта нужно подставить во внешний интеграл:
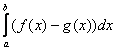
Более компактная запись всего решения выглядит так:
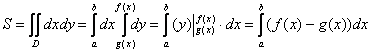
Полученная формула 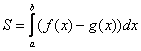 – это в
точности рабочая формула для вычисления площади плоской
фигуры с помощью обычного определённого интеграла! – это в
точности рабочая формула для вычисления площади плоской
фигуры с помощью обычного определённого интеграла!
То есть, задача вычисления площади с помощью двойного интеграла мало чем отличается от задачи нахождения площади с
помощью определённого интеграла!
Пример 9
С помощью двойного интеграла, вычислить площадь фигуры 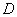 , ограниченной линиями , ограниченной линиями 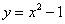 , , 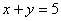
Решение: изобразим область 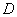 на чертеже: на чертеже:
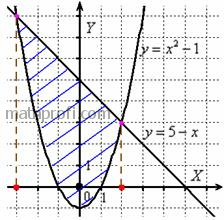
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
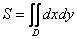
Выберем следующий порядок обхода области (1-й способ):
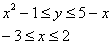
Здесь и далее я не буду останавливаться на том, как выполнять обход, т.к. выше были приведены очень подробные
разъяснения.
Таким образом:
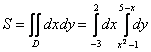
Как уже отмечалось, начинающим лучше вычислять повторные интегралы по отдельности, этого же метода буду
придерживаться и я:
1) Сначала разбираемся с внутренним интегралом:
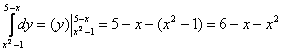
Здесь мы ВМЕСТО «игрек» сначала подставили верхний предел интегрирования 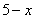 , а затем – нижний: , а затем – нижний: 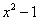 . Если вы запамятовали формулу Ньютона-Лейбница, обязательно
найдите её в приложениях! На всякий случай я приложил к данному курсу Справку по интегралам и
Справку по производным. . Если вы запамятовали формулу Ньютона-Лейбница, обязательно
найдите её в приложениях! На всякий случай я приложил к данному курсу Справку по интегралам и
Справку по производным.
2) Результат, полученный на первом шаге, подставляем во внешний интеграл:
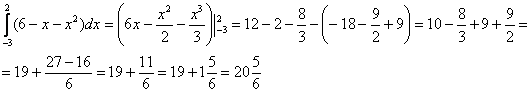
Пункт 2 – это фактически нахождение площади плоской фигуры с
помощью определённого интеграла. Обо всех тонкостях решения этой задачи (а их немало) можно ознакомиться по ссылке
выше либо в курсе Определённые и несобственные интегралы.
Это китайское напоминание.
Ответ: 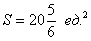
Несмотря на то, что эту задачу мы неоднократно решали ранее, здесь ещё есть о чём поговорить.
Любопытное задание для самостоятельного решения:
Пример 10
С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями 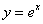 , , 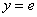 , , 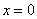
Примерный образец чистового оформления задачи в конце книги.
В двух предыдущих примерах значительно выгоднее использовать первый способ
обхода области, любознательные читатели, кстати, могут изменить порядок обхода и вычислить площади вторым способом. Если
не допустите ошибку, то, естественно, получатся те же самые значения площадей.
Но в ряде случаев более эффективен второй способ обхода области, и в
заключение курса молодого «ботана» рассмотрим ещё пару примеров на эту тему:
Пример 11
С помощью двойного интеграла, вычислить площадь плоской фигуры 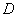 , ограниченной линиями , ограниченной линиями 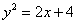 , , 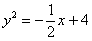
Решение: нас с нетерпением ждут две параболы, которые «лежат на боку». Улыбаться не нужно, похожие вещи в
кратных интегралах встречаются частенько.
Представим параболу 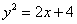 в
виде двух функций: в
виде двух функций:
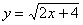 – верхняя ветвь и – верхняя ветвь и 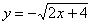 – нижняя ветвь. – нижняя ветвь.
Аналогично, представим параболу 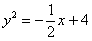 в виде верхней в виде верхней 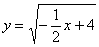 и нижней и нижней 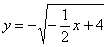 ветвей. ветвей.
Графики строим поточечно, причём, по причине симметрии, вычислений у нас в два раза меньше. В результате получается вот
такая причудливая фигура:
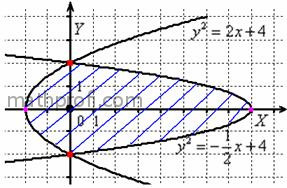
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
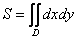
Что будет, если мы выберем первый способ обхода области? Во-первых,
данную область придётся разделить на две части. А во-вторых, мы будем наблюдать сию печальную картину: 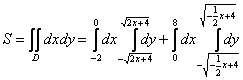 (следим по чертежу!!!). Интегралы, конечно,
не «убийственные», но… есть старая математическая присказка: кто с корнями дружен, тому зачёт не нужен. (следим по чертежу!!!). Интегралы, конечно,
не «убийственные», но… есть старая математическая присказка: кто с корнями дружен, тому зачёт не нужен.
Поэтому из недоразумения, которое дано в условии, выразим обратные функции:
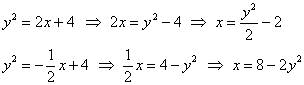
Обратные функции в данном примере обладают тем преимуществом, что задают сразу всю параболу целиком без
всяких там веток, корней и прочего дерева.
И, согласно второму способу, обход области будет следующим:
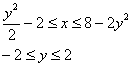
Таким образом:
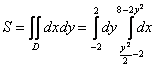
Как говорится, ощутите разницу.
1) Расправляемся с внутренним интегралом:
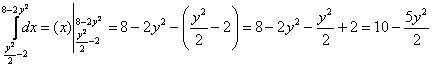
Результат подставляем во внешний интеграл:
2) 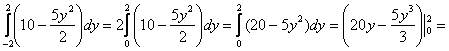
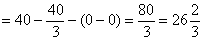
Интегрирование по переменной «игрек» не должно смущать, была бы буква «зю» – замечательно бы проинтегрировалось и по ней.
Также обратите внимание на первый шаг: подынтегральная функция 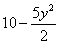 является чётной, а отрезок интегрирования симметричен относительно
нуля. Поэтому отрезок можно споловинить, а результат – удвоить. Что добавить…. Всё! является чётной, а отрезок интегрирования симметричен относительно
нуля. Поэтому отрезок можно споловинить, а результат – удвоить. Что добавить…. Всё!
Ответ: 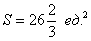
Для проверки своей техники интегрирования можете попробовать вычислить 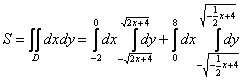 . Ответ должен получиться точно таким же. . Ответ должен получиться точно таким же.
Пример 12
С помощью двойного интеграла, вычислить площадь плоской фигуры, ограниченной линиями 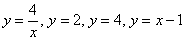
Это пример для самостоятельного решения. Интересно отметить, что если вы попробуете использовать первый способ обхода
области, то фигуру придётся разделить уже не на две, а на три части! И, соответственно, получится три пары повторных
интегралов. Бывает и такое.
Итак, начальный мастер-класс подошёл к завершению, и пора переходить на гроссмейстерский уровень. Обязательно с хорошим
настроением! – оранжевым настроением – прямо как сейчас у меня, а почему оно такое, я объясню чуть позже:
 1.4. Как вычислить произвольный двойной интеграл? 1.4. Как вычислить произвольный двойной интеграл?
 1.2.1. Как изменить порядок обхода области? 1.2.1. Как изменить порядок обхода области?
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
|