|
Блиц-курс – Кратные и криволинейные интегралы |
1.1.2. Как решить двойной интеграл? Повторные интегралыДля того чтобы вычислить двойной интеграл, его нужно свести к так называемым повторным интегралам. Сделать это можно двумя способами. Наиболее распространён следующий способ: Откуда взять пределы интегрирования? Они зависят от того, какая в условии задачи дана область После того, как переход к повторным интегралам осуществлён, следуют непосредственно вычисления: сначала берётся внутренний интеграл Грубо говоря, решение сводится к вычислению двух определённых интегралов. Как видите всё не так сложно и страшно, и если вы совладали с «обыкновенным» определённым интегралом, что мешает разобраться с двумя интегралами?! Второй способ перехода к повторным интегралам встречается несколько реже: Что поменялось? Поменялся порядок интегрирования: теперь внутренний интеграл берётся по «икс», а внешний – по «игрек». Пределы интегрирования, обозначенные звёздочками – будут другими! (в общем случае). Одиночные звёздочки внешнего интеграла – это числа, а двойные звёздочки внутреннего интеграла – это обратные функции Какой бы мы ни выбрали способ перехода к повторным интегралам, Пожалуйста, запомните это важное свойство, которое можно использовать, в том числе, для проверки решения.
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за пару дней!
Научись решать за пару дней!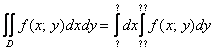
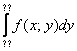 , а потом – внешний. Друг за другом. Отсюда и название – повторные интегралы.
, а потом – внешний. Друг за другом. Отсюда и название – повторные интегралы.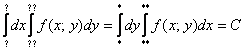
 1.1.3. Алгоритм решения двойного интеграла
1.1.3. Алгоритм решения двойного интеграла 1.1.1. Что значит решить двойной интеграл?
1.1.1. Что значит решить двойной интеграл?