2.5. Несобственные интегралы второго рода
Это интегралы от неограниченных (сверху и / или снизу) функций. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: 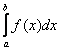 . Но, в отличие от определенного интеграла, подынтегральная функция . Но, в отличие от определенного интеграла, подынтегральная функция 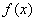 терпит бесконечный разрыв: 1) в точке терпит бесконечный разрыв: 1) в точке 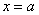 , 2) или в точке , 2) или в точке 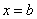 , 3) или в обеих точках сразу, 4) или разрывы даже есть внутри. , 3) или в обеих точках сразу, 4) или разрывы даже есть внутри.
На практике гораздо чаще и одинаково часто встречаются первые два варианта, и сейчас я подброшу монетку… так, начинаем, со Случая 1, когда подынтегральной функции не существует в точке 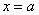 . .
Сразу пример, чтобы было понятно: 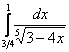 . Вроде бы это определенный интеграл. Но на самом деле нет – это несобственный интеграл второго рода: если мы подставим в подынтегральную функцию значение нижнего предела . Вроде бы это определенный интеграл. Но на самом деле нет – это несобственный интеграл второго рода: если мы подставим в подынтегральную функцию значение нижнего предела 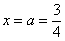 , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке! , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Проверим заодно и верхний предел: 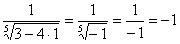 . Здесь всё хорошо. И вообще, обязательно анализируем весь знаменатель, а то, может статься, точки разрыва есть и внутри отрезка . Здесь всё хорошо. И вообще, обязательно анализируем весь знаменатель, а то, может статься, точки разрыва есть и внутри отрезка 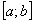 (и это не выдумки). В нашем примере знаменатель обращается в ноль в единственной точке, а значит, вопрос закрыт. (и это не выдумки). В нашем примере знаменатель обращается в ноль в единственной точке, а значит, вопрос закрыт.
Принципиально этот случай выглядит так:
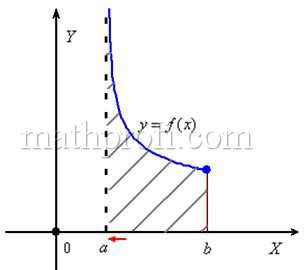
И здесь почти всё так же, как в интеграле первого рода. Если интеграл 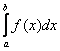 существует, то он численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо он равен конечному числу (площадь бесконечной фигуры – конечна!). существует, то он численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо он равен конечному числу (площадь бесконечной фигуры – конечна!).
Осталось модифицировать формулу Ньютона-Лейбница, я приведу упрощённый по сравнению с учебниками вариант, без лишних букв:
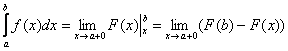
«Добавка» 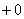 символизирует тот факт, что к точке разрыва мы приближаемся справа (красная стрелка на чертеже). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел. символизирует тот факт, что к точке разрыва мы приближаемся справа (красная стрелка на чертеже). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.
Разделаемся с демонстрационным интегралом:
Пример 35
Вычислить несобственный интеграл или установить его расходимость.

Во-первых, ПИСЬМЕННО констатируем тот факт, что подынтегральная функция терпит бесконечный разрыв в точке 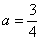 . Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия. . Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
И приём стар, как чешуя динозавра: сначала всегда можно найти первообразную .
Особенно, если пример не прост и особенно в кубе, если вы «чайник».
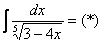
Проведём замену: 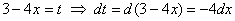 , откуда выражаем оставшийся кусок исходного интеграла, сиротливый дифференциал: , откуда выражаем оставшийся кусок исходного интеграла, сиротливый дифференциал: 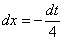
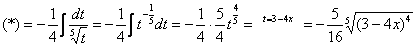
Проверка: 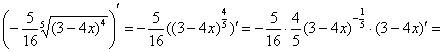
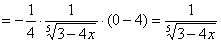 , в чём мы и хотели убедиться. , в чём мы и хотели убедиться.
Теперь вычислим несобственный интеграл, сначала решение, затем комментарии:
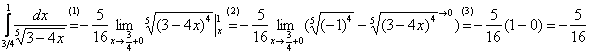
(1) Используем формулу 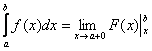
(2) и её продолжение 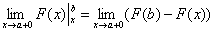 , где при подстановке нижнего предела интегрирования вместо «икс» мы формально подставляем «икс». , где при подстановке нижнего предела интегрирования вместо «икс» мы формально подставляем «икс».
(3) Но самое главное: как выяснить, куда стремится 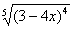 , если , если 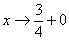 ? Всё просто. Мысленно либо на черновике подставляем ? Всё просто. Мысленно либо на черновике подставляем 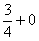 под корень и проводим упрощения: под корень и проводим упрощения: 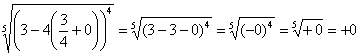 – в результате получено бесконечно малое положительное значение, поэтому – в результате получено бесконечно малое положительное значение, поэтому 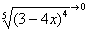 . .
Результат получился отрицательным, и в этом нет криминала, просто соответствующая криволинейная трапеция расположена под осью  . .
Решение можно оформить и по-другому. Например, провести ту же замену прямо в несобственном интеграле с пересчётом новых пределов интегрирования. Ну и совсем шикарно обыденно – это с ходу подвести под знак дифференциала:
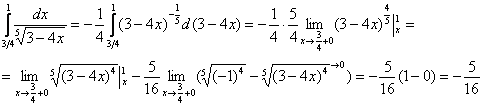
А сейчас два интеграла для самостоятельного решения:
Пример 36
Вычислить несобственные интегралы или установить их расходимость
а) 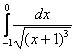 , б) , б) 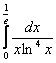
В образце я привёл прямое решение с подведением под знак дифференциала и подробно закомментировал что, к чему и почему стремится. Обязательно разберитесь!
Случай 2. Если подынтегральной функции не существует в точке 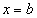 . .
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит так:
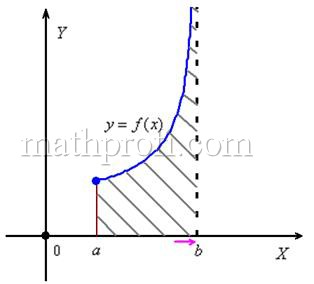
Здесь всё аналогично, только переменная «икс» стремится к значению 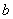 слева: слева:
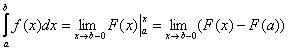
Такой предел называют левосторонним, и бесконечно малая отрицательная «добавка» 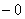 означает, что к точке «бэ» мы подбираемся по оси означает, что к точке «бэ» мы подбираемся по оси 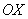 именно слева. именно слева.
Пример 37
Вычислить несобственный интеграл или установить его расходимость.
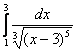
Очевидно, что подынтегральная функция терпит бесконечный разрыв в точке 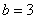 , но не пренебрегаем и проверяем, что больше разрывов нет! – по той причине, что знаменатель обращается в ноль в единственной точке. , но не пренебрегаем и проверяем, что больше разрывов нет! – по той причине, что знаменатель обращается в ноль в единственной точке.
Интеграл решим методом подведения под знак дифференциала:
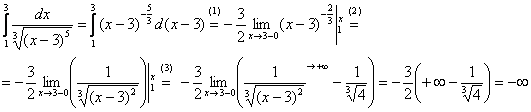
(1) Берём интеграл и используем формулу 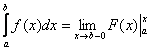 . Наверное, вы обратили внимание, что саму формулу на чистовик записывать не обязательно. Все эти формулы носят частный характер и не предназначены даже для запоминания – самое главное, ПОНИМАТЬ, что происходит в том или ином интеграле, в том или ином случае. Не забываем быстренько выполнить черновую проверку: . Наверное, вы обратили внимание, что саму формулу на чистовик записывать не обязательно. Все эти формулы носят частный характер и не предназначены даже для запоминания – самое главное, ПОНИМАТЬ, что происходит в том или ином интеграле, в том или ином случае. Не забываем быстренько выполнить черновую проверку:
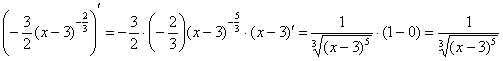 , ОК. , ОК.
(2) Представляем первообразную в более удобном виде.
(3) Подставляем в неё пределы интегрирования: 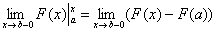 , формально считая, что вместо «икс» мы подставляем «икс». , формально считая, что вместо «икс» мы подставляем «икс».
Как выяснить, что при 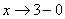 дробь дробь 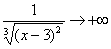 ? Приём тот же самый: мысленно либо на черновике подставляем ? Приём тот же самый: мысленно либо на черновике подставляем 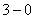 под корень и проводим упрощения: под корень и проводим упрощения:
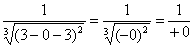 , а единица, делённая на бесконечно малое и положительное значение – это «плюс» бесконечность: , а единица, делённая на бесконечно малое и положительное значение – это «плюс» бесконечность: 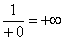 . .
И на завершающем шаге бесконечность меняет знак: 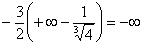
Будьте очень внимательны в знаках! Да, конечно, несобственный интеграл расходится, но 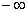 и и 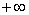 – это две разные вещи, и если вы недосмотрите за знаками, то допустите серьезную ошибку. – это две разные вещи, и если вы недосмотрите за знаками, то допустите серьезную ошибку.
Следующие интегралы для самостоятельного рассмотрения:
Пример 38
Вычислить несобственные интегралы или установить их расходимость.
а) 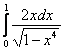 , б) , б) 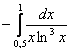
В образце решения я опять использовал «быстрый» способ, но если вам трудно, то, конечно, сначала лучше найти первообразную.
И в заключение курса коротко о более редких случаях:
 2.6. Когда разрывы на обоих концах и / или внутри отрезка интегрирования 2.6. Когда разрывы на обоих концах и / или внутри отрезка интегрирования
 2.4. Что делать, если оба предела интегрирования бесконечны? 2.4. Что делать, если оба предела интегрирования бесконечны?
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
|

 Научись решать за ОДИН день!
Научись решать за ОДИН день! . Но, в отличие от определенного интеграла, подынтегральная функция
. Но, в отличие от определенного интеграла, подынтегральная функция 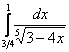 . Вроде бы это определенный интеграл. Но на самом деле нет – это несобственный интеграл второго рода: если мы подставим в подынтегральную функцию значение нижнего предела
. Вроде бы это определенный интеграл. Но на самом деле нет – это несобственный интеграл второго рода: если мы подставим в подынтегральную функцию значение нижнего предела 
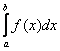 существует, то он численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо он равен конечному числу (площадь бесконечной фигуры – конечна!).
существует, то он численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо он равен конечному числу (площадь бесконечной фигуры – конечна!). 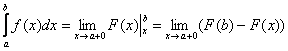

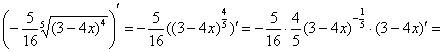
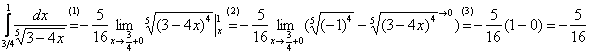
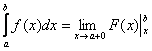
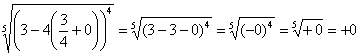 – в результате получено бесконечно малое положительное значение, поэтому
– в результате получено бесконечно малое положительное значение, поэтому 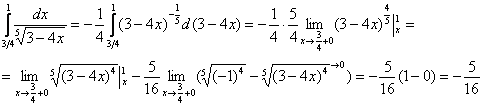
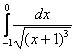 , б)
, б) 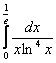

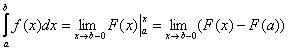
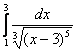
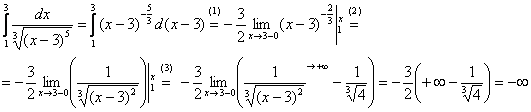
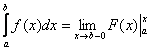 . Наверное, вы обратили внимание, что саму формулу на чистовик записывать не обязательно. Все эти формулы носят частный характер и не предназначены даже для запоминания – самое главное, ПОНИМАТЬ, что происходит в том или ином интеграле, в том или ином случае. Не забываем быстренько выполнить черновую проверку:
. Наверное, вы обратили внимание, что саму формулу на чистовик записывать не обязательно. Все эти формулы носят частный характер и не предназначены даже для запоминания – самое главное, ПОНИМАТЬ, что происходит в том или ином интеграле, в том или ином случае. Не забываем быстренько выполнить черновую проверку: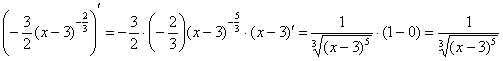 , ОК.
, ОК.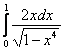 , б)
, б) 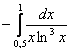
 2.6. Когда разрывы на обоих концах и / или внутри отрезка интегрирования
2.6. Когда разрывы на обоих концах и / или внутри отрезка интегрирования 2.4. Что делать, если оба предела интегрирования бесконечны?
2.4. Что делать, если оба предела интегрирования бесконечны?