|
Экстремально короткий курс по интегралам |
2.4. Что делать, если оба предела интегрирования бесконечны?Интеграл Пример 32 Подынтегральная функция непрерывна всюду, и прямое решение таково: Второй, более академичный способ состоит в том, чтобы разделить интеграл на две части, обычно в качестве точки «распила» выбирают ноль: Теперь обратим внимание на подынтегральную функцию. Она является чётной и промежуток интегрирования симметричен относительно нуля. Знакомая геометрия: Переходим к ещё более любопытному случаю: Подынтегральная функция всюду непрерывна, нечётна и промежуток интегрирования симметричен относительно нуля. Но пользоваться этим НЕЛЬЗЯ, поскольку интеграл от такой функции может быть вовсе не определён. Как в нашем случае – по той причине: Почему? Потому что переменная «а» может стремиться к «минус» бесконечности, например, БЫСТРЕЕ, чем переменная «бэ» к «плюс» бесконечности. Или наоборот. К такому же выводу можно прийти, если распилить пациента на две части: Следует отметить, что в теории рассматривается особый случай – когда обе переменные стремятся к бесконечностям с одинаковой скоростью. Это выражается пределом: Но это имеет смысл включать в решение тогда, когда вы учитесь сильно углублённо :) В «массовой» же практике такие вещи ни к чему, а посему просто даём ответ, что значение интеграла не определено. Тонкость же состоит в том, что несобственные интегралы Пример 34 Это пример для самостоятельного решения. Но на практике, разумеется, функция не обязана быть чётной или нечётной, пожалуйста:
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!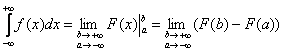 – предел с двумя «динамическими» переменными, и давайте рассмотрим больше такой демонстрационный интеграл:
– предел с двумя «динамическими» переменными, и давайте рассмотрим больше такой демонстрационный интеграл: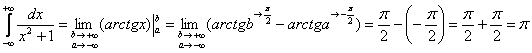
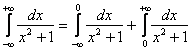
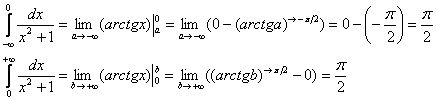
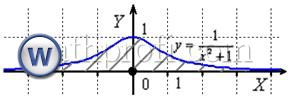
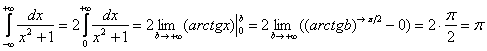
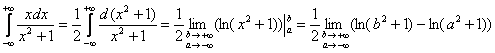 – что этого предела не существует. Он не определён.
– что этого предела не существует. Он не определён.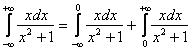
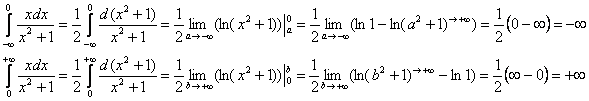
 сходятся, равны по модулю и противоположны по знаку (в силу нечётности функции):
сходятся, равны по модулю и противоположны по знаку (в силу нечётности функции): 2.5. Несобственные интегралы второго рода
2.5. Несобственные интегралы второго рода 2.3. Несобственный интеграл с бесконечным нижним пределом
2.3. Несобственный интеграл с бесконечным нижним пределом