2.6. Когда разрывы на обоих концах
и / или внутри отрезка интегрирования
Итак, тот же интеграл 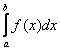 , но разрывы уже на обоих концах отрезка. По аналогии с несобственными интегралами 1-го рода, здесь можно записать двухстаночный предел, и мне таки придётся добавить пару новых букв, «эпсилон» и «ню»: , но разрывы уже на обоих концах отрезка. По аналогии с несобственными интегралами 1-го рода, здесь можно записать двухстаночный предел, и мне таки придётся добавить пару новых букв, «эпсилон» и «ню»:
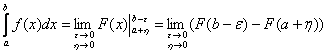
Но усложнять оформление мы не будем, ведь такой интеграл можно разделить на две части – с дальнейшим вычислением знакомых интегралов. А иногда всё ещё проще.
Редко, да метко, и, между прочим, задачка с «заочки»… прям как Маяковский:)
Пример 39
Вычислить несобственный интеграл или установить его расходимость

Подынтегральная функция терпит бесконечные разрывы на обоих концах отрезка интегрирования, но это не помеха:
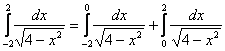 – и в то же время помеха :) – и в то же время помеха :)
Поскольку подынтегральная функция является чётной, а промежуток интегрирования симметричен относительно нуля, то… правильно представили:
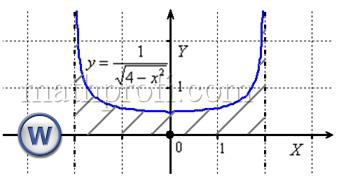
И чётностью пользоваться МОЖНО. Ибо если одна половинка конечна или бесконечна, то другая – такая же. Поэтому не будем допускать математический грех, интеграл споловиним, а результат удвоим:
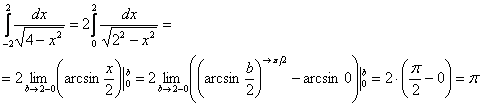
опять это удивительное значение…
Следующий интеграл для самостоятельного решения:
Пример 40
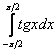
Точно так же, как у аналогичных интегралов 1-го рода, нечетностью функции пользоваться НЕЛЬЗЯ. Да, если интеграл сходится, то он действительно будет равен нулю, но если расходится, то… – смотрите образец решения!
Но, разумеется, подынтегральная функция может оказаться «обычной», да и промежуток интегрирования не симметричным относительно нуля:
Пример 41

Так как подынтегральная функция отрицательна на интервале 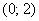 , то сразу можно сказать, что результат (конечный или бесконечный) должен получиться отрицательным. И алгоритм тот же, делим интеграл на две части: , то сразу можно сказать, что результат (конечный или бесконечный) должен получиться отрицательным. И алгоритм тот же, делим интеграл на две части:

Чтобы не «таскать за собой» пределы интегрирования, сначала удобно найти неопределённый интеграл. Выделяем полный квадрат в знаменателе и используем табличную формулу 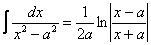 – с той поправкой что ВМЕСТО – с той поправкой что ВМЕСТО 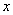 у нас у нас 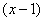 : :
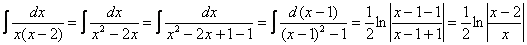
Контроль: 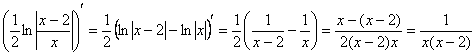
Вычислим первый интеграл – с разрывом в точке 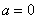 : :
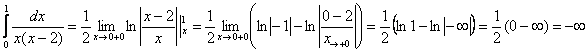
Разберитесь, что куда стремится! И второй интеграл, с разрывом 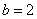 : :
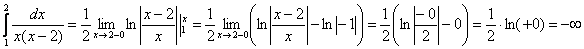
Таким образом: 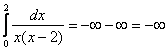 , т.е. несобственный интеграл расходится. , т.е. несобственный интеграл расходится.
Как быть, если точка разрыва находится прямо на отрезке интегрирования? Точно так же! Алгоритм такой же, самостоятельно:
Пример 42
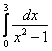
Встречаются ли такие примеры на практике? Да, реально встречаются, и поэтому со всей серьёзностью отнеситесь к этим, вроде бы несерьёзным примерам.
Следует отметить, что для интегралов 2-го рода тоже вводится понятие сходимости по Коши, но эту информацию я оставлю за кадром, т.к. она не входит в аптечку скорой математической помощи. И напоследок что-нибудь вкусное:
 2.7. Интегралы-«ассорти» 2.7. Интегралы-«ассорти»
 2.5. Несобственные интегралы второго рода 2.5. Несобственные интегралы второго рода
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
|