|
Экстремально короткий курс по интегралам |
1.6. Метод интегрирования по частям в определенном интегралеЗдесь новизны еще меньше. Почти всё, что справедливо для неопределенного интеграла, справедливо и для определенного интеграла. Плюсом идёт то, что в формуле интегрирования по частям добавляются пределы интегрирования:
Формулу Ньютона-Лейбница здесь нужно применить дважды: для произведения Пример я подобрал не самый простой, но очень и очень познавательный: Пример 8 Сразу начинаем решение и сразу прерываем его «звёздочкой». Этот тип интеграла не встречался ранее, он тоже берётся по частям. Используем стандартную схему интегрирования по частям: Интеграл от квадрата тангенса я разбирал в 1-й части курса, но на чистовике, естественно, всё расписываем подробно, вспоминая заодно насущные тригонометрические формулы: Далее открываем решение и на первом шаге (1) расписываем правую часть формулы (2) Для произведения (3) Берем два оставшихся интеграла. Интеграл (4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных. Далее ответ доводится «до ума». Повторюсь, будьте ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫ при подстановках и заключительных вычислениях. Здесь допускают ошибки чаще всего. Если честно, я недолюбливаю формулу На первом этапе находим первообразную: Интегрируем по частям:
Первообразная функция найдена. …Кстати, все ли поняли, почему в определённом интеграле не имеет смысла приплюсовывать константу В чём преимущество такого похода? Не нужно «таскать за собой» пределы интегрирования, действительно, замучаться можно десяток раз записывать мелкие значки пределов интегрирования. На втором этапе проводим проверку (обычно на черновике). Тоже логично. Ведь если неправильно найдена первообразная, то… правильно! И это лучше выяснить немедленно, дифференцируем ответ: И третий этап – применение формулы Ньютона-Лейбница: Здесь тоже есть существенная выгода! – это гораздо меньший риск запутаться в подстановках и вычислениях, т. к. формула Ньютона-Лейбница применяется всего лишь один раз. Рассмотренный алгоритм решения И нужно, если интеграл трудный. Так, если «чайник» решит разобранный интеграл по формуле Уважаемый студент, распечатай и наклей рядом с формулой Ньютона-Лейбница: 1) Сначала находим первообразную функцию 2) Проверяем найденную первообразную дифференцированием. Здесь, кстати, может статься, позабылись производные – и тогда самое время подтянуть свои навыки! 3) Используем формулу Ньютона-Лейбница. Все вычисления проводим ПРЕДЕЛЬНО ВНИМАТЕЛЬНО – тут самое слабое звено задания. Царь тут! И на холодную закуску интеграл для самостоятельного решения. Пример 9
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!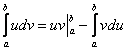
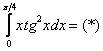
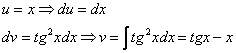
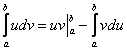 :
: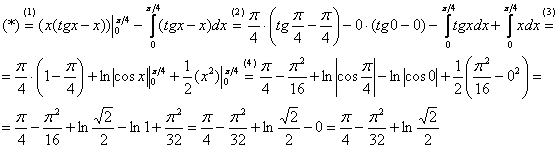
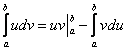 и, по возможности, … обхожусь вообще без нее! Рассмотрим второй способ решения, который, с моей точки зрения, более рационален:
и, по возможности, … обхожусь вообще без нее! Рассмотрим второй способ решения, который, с моей точки зрения, более рационален: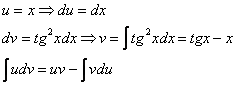
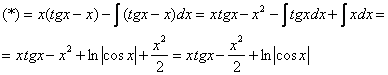
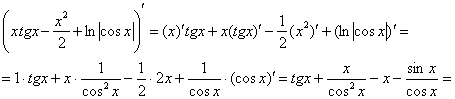
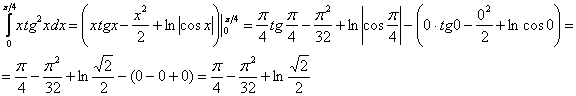
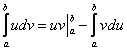 (1-м способом), то 95% где-нибудь допустит ошибку.
(1-м способом), то 95% где-нибудь допустит ошибку.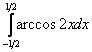
 1.7. Геометрический смысл определённого интеграла
1.7. Геометрический смысл определённого интеграла 1.5. А если подвести функцию под знак дифференциала?
1.5. А если подвести функцию под знак дифференциала?