|
Экстремально короткий курс по интегралам |
1.5. А если подвести функцию под знак дифференциала?Как вы помните, это ускоренная реализация тех же действий – своеобразная «замена без замены». И если мы подводим функцию под знак дифференциала, то менять пределы интегрирования не нужно! Почему? Потому что в этом случае нет фактического перехода к новой переменной. Недавний пациент: Таким образом, если определённый интеграл не очень сложен, Это быстрее, это компактнее в оформлении, и на самом деле – это обыденность, в чём вы убедитесь десятки раз. И раза так два-три прямо сейчас :) Пример 7 Не пропускаем задания!! ;), и обязательно сверяемся в конце книги.
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!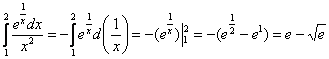 , то есть, вместо академичной замены
, то есть, вместо академичной замены 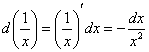 и добавить минус перед интегралом, чтобы в результате раскрытия дифференциала получился исходный интеграл. И ещё могут возникнуть непонятки с интегрированием – в этом случае удобно МЫСЛЕННО обозначить
и добавить минус перед интегралом, чтобы в результате раскрытия дифференциала получился исходный интеграл. И ещё могут возникнуть непонятки с интегрированием – в этом случае удобно МЫСЛЕННО обозначить 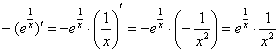 .
.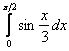 , б)
, б) 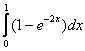 , в)
, в)  1.6. Метод интегрирования по частям в определенном интеграле
1.6. Метод интегрирования по частям в определенном интеграле 1.4. Замена переменной в определенном интеграле
1.4. Замена переменной в определенном интеграле