|
Экстремально короткий курс по интегралам |
1.2. Некоторые свойства определённого интегралаВ этом маленьком параграфе я перечислю свойства, которые имеют большое значение для практики. 1. В определенном интеграле можно переставить верхний и нижний предел интегрирования, сменив при этом знак:
2. Как и для неопределенного интеграла, для определённого интеграла справедливо свойство линейности. Это свойство состоит в двух правилах:
* Напоминаю, что разность – есть алгебраическая сумма: 3. Для определенного интеграла работает формула интегрирования по частям: 4. В определенном интеграле можно проводить замену переменной интегрирования и подводить под знак дифференциала. Но по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы поговорим в соответствующем параграфе. Разумеется, существуют и другие свойства, но для ближайшей практики этого вполне достаточно. И она никогда не была так близкА:
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!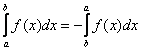
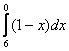 перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок:
перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок: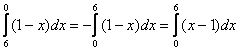 – в таком виде интегрировать значительно удобнее.
– в таком виде интегрировать значительно удобнее. 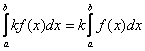 , где
, где 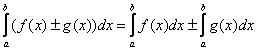 – данное правило справедливо не только для двух, но и для бОльшего количества слагаемых*, например, для трёх:
– данное правило справедливо не только для двух, но и для бОльшего количества слагаемых*, например, для трёх: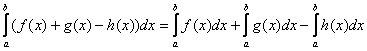
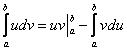
 1.3. Простейшие определённые интегралы
1.3. Простейшие определённые интегралы 1.1. Понятие определённого интеграла
1.1. Понятие определённого интеграла