|
Экстремально короткий курс по интегралам |
1.7. Геометрический смысл определённого интегралаНачнем с криволинейной трапеции. Криволинейной трапецией называется плоская фигура, ограниченная осью В самом начале курса я говорил, что определенный интеграл – это число. А сейчас пришла пора констатировать еще один полезный факт. С точки зрения геометрии, это число – есть ПЛОЩАДЬ. Рассмотрим, например, определенный интеграл И вообще, любому определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры. Эта фигура не обязательно расположена выше оси абсцисс, она может располагаться и ниже, может располагаться и там и там; может быть более простой или более сложной. В простых случаях (квадрат, треугольник и т.д.) площадь легко рассчитывается по «школьным» формулам, но что делать в случаях остальных? Привлечь на помощь определённый интеграл! Рассмотрим самую популярную и самую распространенную тематическую задачу:
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!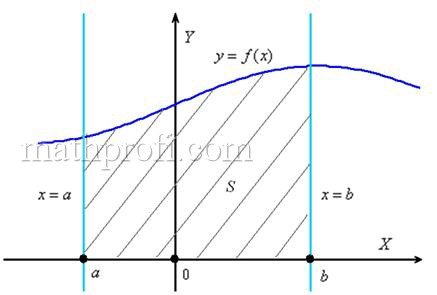
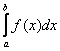 численно равен площади (заштрихована на чертеже) этой криволинейной трапеции. Площадь, как многие помнят, стандартно обозначается буквой
численно равен площади (заштрихована на чертеже) этой криволинейной трапеции. Площадь, как многие помнят, стандартно обозначается буквой  1.8. Как вычислить площадь фигуры с помощью определённого интеграла?
1.8. Как вычислить площадь фигуры с помощью определённого интеграла? 1.6. Метод интегрирования по частям в определенном интеграле
1.6. Метод интегрирования по частям в определенном интеграле