|
Экстремально короткий курс по интегралам |
2.3. Несобственный интеграл с бесконечным нижним пределомОн выглядит так: Пример 30 Во-первых, обращаем внимание, что подынтегральная функция непрерывна на Сам интеграл берётся по частям, и, в принципе, для несобственных интегралов можно записать специальные формулы. Но это уже будет немножко извращение, так как гораздо проще найти первообразную, и затем всё остальное:
Не ленимся, выполняем проверку, по правилу дифференцирования произведения: И, наконец, несобственный интеграл, тут нужно быть аккуратным в знаках: Самостоятельно: Пример 31
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!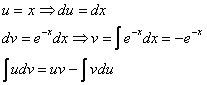
 2.4. Что делать, если оба предела интегрирования бесконечны?
2.4. Что делать, если оба предела интегрирования бесконечны? 2.2. Несобственный интеграл первого рода
2.2. Несобственный интеграл первого рода