|
Экстремально короткий курс по интегралам |
2.1. Понятие несобственного интегралаЭто «родственник» определённого интеграла. …Нормальное такое определение :). И сразу возникает вопрос: чем отличается несобственный интеграл от «собрата»? Он может отличаться пределами интегрирования: Такие интегралы получили название несобственные интегралы первого рода. Кроме того, несобственный интеграл может быть «внешне похож» на определённый интеграл и иметь вид Это так называемые несобственные интегралы второго рода. Что значит решить несобственный интеграл? В отличие от определённого интеграла, тут есть три варианта. Решить несобственный интеграл – это значит найти конечное число, либо получить бесконечность, либо выяснить, что несобственного интеграла не существует. 1) Если несобственный интеграл равен конечному числу, то говорят, что он сходится. Число может быть как положительным, так и отрицательным. Или нулём. 2) Если несобственный интеграл равен бесконечности (со знаком «плюс» или «минус»), то говорят, он расходится. 3) И в ряде случаев несобственного интеграла может вовсе не существовать. Даже если подынтегральная функция непрерывна на промежутке интегрирования! (вспоминаем, что определённый интеграл при этом условии существует всегда). Как решить несобственный интеграл? С помощью той же формулы Ньютона-Лейбница. С некоторыми особенностями. И здесь вы должны понимать и уметь решать несложные пределы функций. В чём смысл несобственного интеграла? Геометрически – это тоже площадь (если интеграл существует). Но площадь своеобразная. И с этим своеобразием мы познакомимся прямо на следующей странице:
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!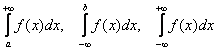 – то есть, один или даже оба предела бесконечны, при этом подынтегральная функция непрерывна на промежутке интегрирования.
– то есть, один или даже оба предела бесконечны, при этом подынтегральная функция непрерывна на промежутке интегрирования.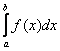 . Но есть один нюанс. Подынтегральная функция не определена в точке
. Но есть один нюанс. Подынтегральная функция не определена в точке  2.2. Несобственный интеграл первого рода
2.2. Несобственный интеграл первого рода 1.11. А если подынтегральная функция нечётная?
1.11. А если подынтегральная функция нечётная?