|
Экстремально короткий курс по интегралам |
1.11. А если подынтегральная функция нечётная?Вам понравится ещё больше :) Кратко напомню, что нечётная функция характеризуется свойством
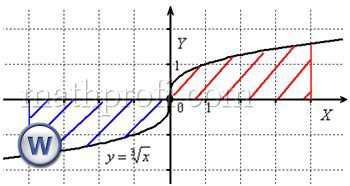
Если подынтегральная функция Рассмотрим очередной пример с иллюстрацией, и заодно я продолжу знакомить вас с графиками функций, которые не встречались ранее: График функции График любой нечётной функции симметричен относительно начала координат, в частности: 1) Любой определенный интеграл – это всё равно формально площадь (пусть даже отрицательная). Поэтому 2) Задача на нахождение площади – это совершенно другая задача. Так, если бы нам было предложено найти площадь фигуры в данном примере, то её следовало бы вычислить следующим образом: Применять ли рассмотренное свойство на практике? На самом деле вопрос не так прост, как кажется. Когда вам предложен сложный пример с большим количеством вычислений, то можно, и даже уместно указать, что такой интеграл равен нулю, сославшись на нечетность функции и симметричность промежутка интегрирования относительно нуля. Как говорится, знание – сила, а незнание – рабочая сила. Но когда вам предложен короткий пример, то лучше «прикинуться простачком» и решить его подробно:
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!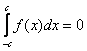 . Такие интегралы можно встретить довольно часто:
. Такие интегралы можно встретить довольно часто: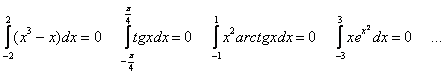
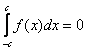 , так как в силу нечётности функции
, так как в силу нечётности функции 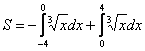
 2.1. Понятие несобственного интеграла
2.1. Понятие несобственного интеграла 1.10. Интеграл от чётной функции по симметричному относительно нуля отрезку
1.10. Интеграл от чётной функции по симметричному относительно нуля отрезку