|
Экстремально короткий курс по интегралам |
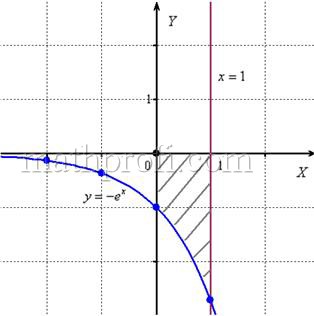
1.8. Как вычислить площадь с помощью определённого интеграла?Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так: Пример 10 И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций. В нашей задаче: прямая Искомую фигуру желательно штриховать: Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке Ответ: После того, как задание выполнено, полезно взглянуть на чертёж И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно. Пример 11 Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью Пример 12 Решение: найдём несколько опорных точек для построения экспоненты: Ответ: На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам: Пример 13 Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой». С прямой Выполним чертеж: А теперь рабочая формула: если на отрезке Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ. В нашем примере очевидно, что на отрезке Завершение решения может выглядеть так: На отрезке Ответ: Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы А сейчас пара типовых задач для самостоятельного решения Пример 14 а) б) Решение с чертежами и краткими комментариями в конце книги В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни: Пример 15 Решение: выполним бесхитростный чертёж, Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно: 1) на отрезке Совершенно понятно, что площади можно (и нужно) сложить: Ответ: И познавательный пример для самостоятельного решения: Пример 16 Итак, систематизируем важные моменты этой задачи: На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией. Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой Во-вторых, не всегда понятен «внешний вид» линии, и функция После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части. Составляем определённый интеграл или несколько интегралов по формуле Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница. Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!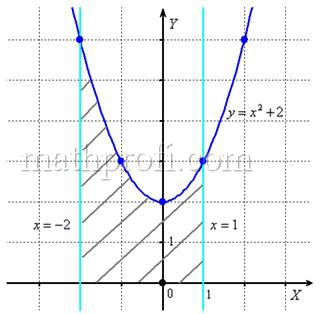
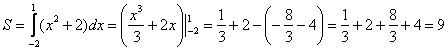
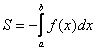 .
.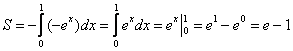
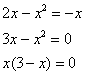
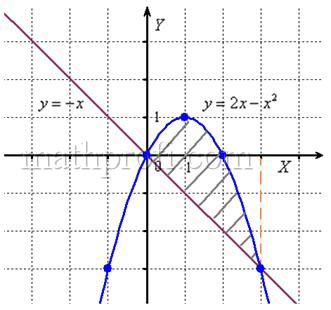
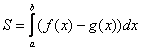
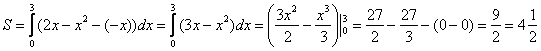
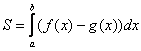 . Поскольку ось
. Поскольку ось 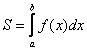 либо
либо 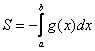
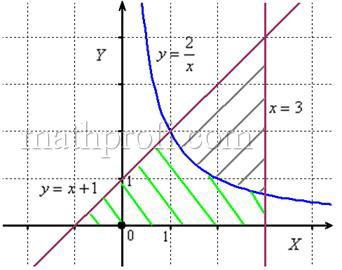
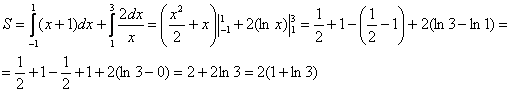
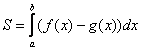 , все основные вариации мы разобрали выше.
, все основные вариации мы разобрали выше. 1.9. Объём тела вращения
1.9. Объём тела вращения 1.7. Геометрический смысл определённого интеграла
1.7. Геометрический смысл определённого интеграла