|
Экстремально короткий курс по интегралам |
1.4. Замена переменной в определённом интегралеДля определенного интеграла справедливы все типы замен, что и для неопределенного интеграла, но иногда её проводить нельзя (о чём позже). Ну а основная новизна состоит в том, как поменять пределы интегрирования при замене? В примерах ниже я постараюсь привести такие типы замен, которые не встречались ранее: Пример 5 Во-первых, замечаем, что отрезок И главный вопрос здесь не в определённом интеграле, а в том, какую подобрать замену. Смотрим в Таблицу интегралов (см. Приложения) и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: Из вышеуказанных соображений совершенно естественно напрашивается замена: Выясняем, во что превратится оставшаяся часть По сравнению с заменой в неопределенном интеграле, у нас добавляется дополнительный этап: находим новые переделы интегрирования. Это достаточно просто. Смотрим на нашу замену Сначала подставляем в И всего-то лишь…. Завершаем решение: (1) В соответствии с проведённой заменой, записываем новый интеграл с новыми пределами интегрирования. (2) Это простейший табличный интеграл, интегрируем по таблице. Константу (3) Используем формулу Ньютона-Лейбница И особенно приятно, что никаких обратных замен проводить не нужно. Пример 6 Решения и ответы в конце книги. Приложение Тригонометрические таблицы в помощь, в изучаемой теме этот справочный материал требуется довольно часто. И теперь обещанный момент о правомерности замены. В определённой ситуации её проводить нельзя! Так, интеграл
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!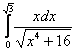
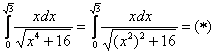 (прерываем решение для промежуточных действий)
(прерываем решение для промежуточных действий)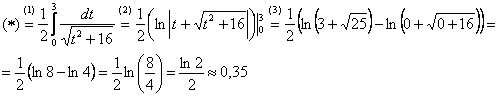
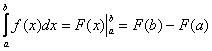 и упрощаем результат по известной формуле.
и упрощаем результат по известной формуле. 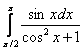 , б)
, б) 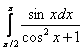 , казалось бы, разрешим с помощью универсальной тригонометрической подстановки
, казалось бы, разрешим с помощью универсальной тригонометрической подстановки  1.5. А если подвести функцию под знак дифференциала?
1.5. А если подвести функцию под знак дифференциала? 1.3. Простейшие определённые интегралы
1.3. Простейшие определённые интегралы