|
Экстремально короткий курс по интегралам |
1.3. Простейшие определённые интегралыНачинаем: Пример 1 Сначала решение, затем комментарии: (1) Выносим константу за знак интеграла. (2) Интегрируем по таблице (см. Приложения) с помощью самой популярной формулы (3) Используем формулу Ньютона-Лейбница Пример 2 Это пример для самостоятельного решения. ОБЯЗАТЕЛЬНО прорешиваем все предлагаемые мной примеры от руки!! Ручка и тетрадь под рукой? Отлично. Кроме того, открываем и освежаем в памяти Таблицу интегралов и Таблицу производных (см. приложения к курсу). …всё получилось? Свериться с решениями можно в конце книги. Также проверьте, есть ли у вас калькулятор. Хотя бы самый простой. Но лучше с функциями (логарифмами, синусами и т.д.). На всякий бедственный случай прилагаю к курсу калькулятор в Экселе. А ещё лучше, если у вас есть калькулятор, который считает обыкновенные дроби. Потому что с дробовиком всё нипочём. …оружие под рукой? Продолжаем! Пример 3 Сначала решение, затем комментарии: (1) Используем свойство линейности определенного интеграла. (2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела. (3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница: СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений, Поэтому будьте внимательны! Особое внимание заостряю на 3-м слагаемом: Следует заметить, что рассмотренный способ решения – не единственный, и при определенном опыте его можно значительно сократить. Примерно так: Здесь устно используем правила линейности, устно интегрируем по таблице и в результате получаем всего лишь одну скобку с отчёркиванием пределов: Какие достоинства у «короткого» способа решения? Быстрота и компактность записи. А недостатки? Повышенный риск допустить ошибку. Поэтому «чайникам» я рекомендую подробное решение. А лучше оба. Для сверки. Кстати, о сверках и проверках. Запомните красное правило: Перед тем, как использовать формулу Ньютона-Лейбница, Ибо, если она найдена неверно, то и всё остальное тоже будет неправильным. Так, применительно к рассмотренному примеру: перед тем, как в первообразную функцию Пример 4 Решаем самостоятельно. И коротко, и подробно.
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!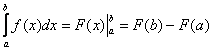 . Сначала подставляем в
. Сначала подставляем в 
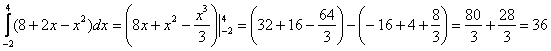
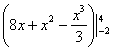 (в отличие от трёх скобок в первом способе). Далее в «цельную» первообразную функцию, сначала подставляем 4, затем –2, опять же выполняя все действия в уме.
(в отличие от трёх скобок в первом способе). Далее в «цельную» первообразную функцию, сначала подставляем 4, затем –2, опять же выполняя все действия в уме. 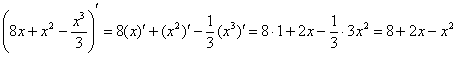 – получена исходная подынтегральная функция, значит, первообразная найдена верно. Теперь можно и формулу Ньютона-Лейбница применить.
– получена исходная подынтегральная функция, значит, первообразная найдена верно. Теперь можно и формулу Ньютона-Лейбница применить.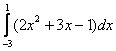
 1.4. Замена переменной в определенном интеграле
1.4. Замена переменной в определенном интеграле 1.2. Некоторые свойства определённого интеграла
1.2. Некоторые свойства определённого интеграла