|
Экстремально короткий курс по интегралам |
2.2. Несобственный интеграл первого родаЭто интеграл с бесконечным (и) пределом интегрирования, и самый популярный на практике вариант таков: Для определённости положим, что И для решения рассматриваемого интеграла нужно немного модифицировать формулу Ньютона-Лейбница В чем отличие от определённого интеграла? Да ни в чём особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию Следует отметить, что строгое определение несобственного интеграла даётся именно через предел, и иногда его не существует. Обратите внимание, что вместо привычной буквы Теперь перейдём к «обычным» задачам и начнём с двух хрестоматийных примеров: Пример 26 В таких заданиях чертежей строить не нужно, но понимания ради:
Не забываем пометить, что Таким образом, чтобы не было «затыков» с простейшими пределами, Чистовое оформление задания может выглядеть так: Подынтегральная функция непрерывна на
Таким образом, несобственный интеграл расходится. ! При оформлении примера всегда указываем, что происходит с подынтегральной функцией – непрерывна она или нет. Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия. Пример 27 Здесь ситуация вроде бы похожа: Надеюсь ни у кого не возникло проблем с табличным интегралом и пониманием того, что при Чистовое оформление примера может быть ещё лаконичнее: Рассмотрим более содержательный пример: Пример 28 Со знаменателем всё хорошо и подынтегральная функция непрерывна на В этом случае целесообразно применить тот же алгоритм, что и для определённого интеграла,… вы точно наклеили его на стену? …Ай-яй-яй – а ведь давно пора организовать дома красный угол высшей математики! 1) Сначала попытаемся найти первообразную функцию
И тут прямо напрашивается навести под корнем порядок, проведём замену
2) Проверим найденную первообразную дифференцированием: 3) И теперь с несобственным интегралом никаких проблем, по формуле Точно так же, как и у «собрата», в несобственном интеграле допустима замена переменной с вычислением новых пределов интегрирования, и поэтому решение можно оформить другим способом:
Подынтегральная функция непрерывна на
Подынтегральная функция непрерывна на Кому как нравится, кому как удобнее! И, конечно, тут нужно учитывать целесообразность того или иного способа – в зависимости от того, простой интеграл попался или посложнее. А сейчас два типовых примера для самостоятельного решения: Пример 29 В пункте «а» используем метод выделения полного квадрата. И обратите внимание на формулировку задания, если оно сформулировано именно так, то, вообще говоря, нужно дать ответ: «сходится», «расходится» или «не существует». На практике встречаются неберущиеся интегралы, и тогда этот вопрос решается не вычислением, а использованием признаков сравнения, которые не вошли в настоящий курс ввиду их малой распространенности в «массовых» работах.
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2025, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!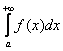 . При этом подынтегральная функция
. При этом подынтегральная функция 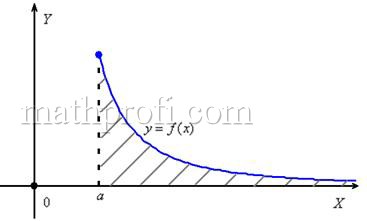
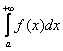 численно равен её площади.
численно равен её площади. 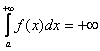 », иными словами, площадь тоже бесконечна. Так быть может. И такой интеграл называют расходящимся (как отмечалось выше). Но. Как это ни парадоксально, площадь бесконечной фигуры может равняться… конечному числу! Например,
», иными словами, площадь тоже бесконечна. Так быть может. И такой интеграл называют расходящимся (как отмечалось выше). Но. Как это ни парадоксально, площадь бесконечной фигуры может равняться… конечному числу! Например, 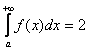 . Такие интегралы называют сходящимися.
. Такие интегралы называют сходящимися.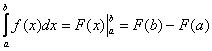 – с поправкой, что
– с поправкой, что 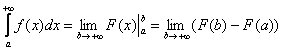
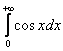 . Несмотря на то, что косинус непрерывен на промежутке
. Несмотря на то, что косинус непрерывен на промежутке 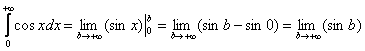 – не существует соответствующего предела.
– не существует соответствующего предела. 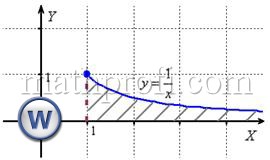
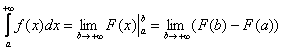 :
:
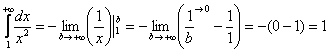 – интеграл сходится, и площадь бесконечной криволинейной трапеции равна конечному числу!
– интеграл сходится, и площадь бесконечной криволинейной трапеции равна конечному числу!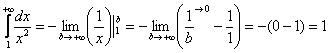
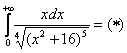
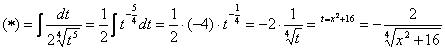
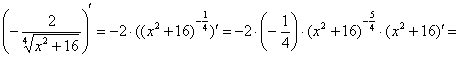
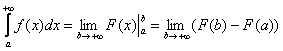 :
: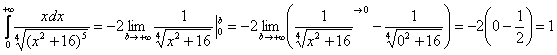
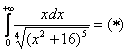
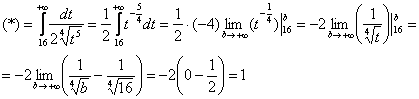
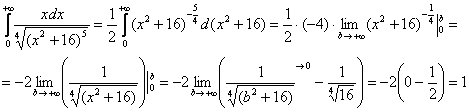
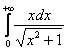
 2.3. Несобственный интеграл с бесконечным нижним пределом
2.3. Несобственный интеграл с бесконечным нижним пределом 2.1. Понятие несобственного интеграла
2.1. Понятие несобственного интеграла