|
Экстремально короткий курс по интегралам |
1.1. Понятие определённого интегралаВ общем виде определенный интеграл записывается так: И перед тем, как перейдём к практике, небольшое faq по теме: Что такое определенный интеграл? С формальной точки зрения, определённый интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число: Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти это число. Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница: Формулу перепишите на листок и наклейте на самом видном месте! Этапы решения определенного интеграла следующие: 1) Сначала находим первообразную функцию 2) Подставляем значение верхнего предела в первообразную функцию: 3) Подставляем значение нижнего предела в первообразную функцию: 4) Рассчитываем (без ошибок!) разность Вопрос следующий, а на самом деле первый: всегда ли существует определенный интеграл? Нет, не всегда. Например, интеграла Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определённого интеграла, желательно убедиться в том, что подынтегральная функция существует и непрерывна* на отрезке интегрирования. Понятие непрерывности понятно даже интуитивно – если график можно начертить, не отрывая карандаша от бумаги, то данная функция непрерывна на этом участке. * Тем не менее, существуют интегралы и от разрывных функций, но они вам вряд ли встретятся (не припоминаю) в типовой практике по теме. В противном случае может получиться такой казус: А сделать надо следующее: предварительно проверить функцию на сущестование и непрерывность. И если для решения (в контрольной работе, на зачете, экзамене) вам предложен несуществующий интеграл вроде Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим посвящена следующая глава. Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике:
Без чего не обходится математика? Конечно же, без всевозможных свойств:
Полную и свежую версию данного курса в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
|
© mathprofi.ru / com, 2010-2026, Высшая математика – просто и доступно! |

 Научись решать за ОДИН день!
Научись решать за ОДИН день!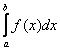
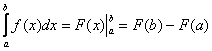
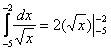 …что делать???! – ведь нельзя же подставлять отрицательные числа под корень!
…что делать???! – ведь нельзя же подставлять отрицательные числа под корень! 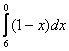 – интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.
– интеграл преспокойно вычисляется по формуле Ньютона-Лейбница. 1.2. Некоторые свойства определённого интеграла
1.2. Некоторые свойства определённого интеграла