1.10. Интеграл от чётной функции
по симметричному относительно нуля отрезку
Сначала вспомним, что такое чётность функции. Функция является чётной, если для неё выполнено условие 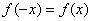 . Для того, чтобы проверить этот факт, ВМЕСТО . Для того, чтобы проверить этот факт, ВМЕСТО 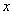 нужно подставить нужно подставить 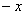 , простейшие примеры: , простейшие примеры:
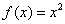 , проверка: , проверка: 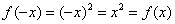 , ,
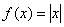 , проверка: , проверка: 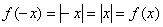 , ,
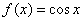 , и он, как многие помнят, тоже чётный: , и он, как многие помнят, тоже чётный: 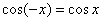 , ,
таким образом, все перечисленные функции являются чётными.
Теперь рассмотрим определённый интеграл вида 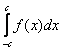 . Легко заметить, что отрезок интегрирования . Легко заметить, что отрезок интегрирования 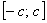 симметричен относительно нуля. симметричен относительно нуля.
Если подынтегральная функция 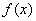 является чётной, то интеграл является чётной, то интеграл 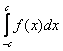 можно вычислить по половине отрезка, а результат – удвоить: можно вычислить по половине отрезка, а результат – удвоить: 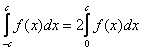 . .
Почему? …догадались? Рассмотрим конкретный пример с чертежом:
Пример 21
Вычислить определенный интеграл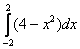
Хоть и очевидно, но проверим функцию 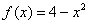 на чётность: на чётность:
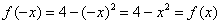
И, согласно правилу, на симметричном относительно нуля отрезке 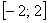 наш интеграл можно «споловинить»: наш интеграл можно «споловинить»:
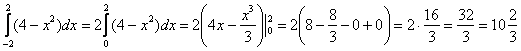
А сейчас геометрическая интерпретация: график любой чётной функция, в частности 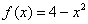 , симметричен относительно оси , симметричен относительно оси  , и теперь-то всем понравится геометрический смысл определённого интеграла:) , и теперь-то всем понравится геометрический смысл определённого интеграла:)
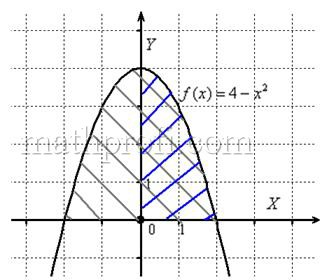
Определенный интеграл 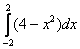 численно равен площади фигуры, которая заштрихована серым цветом. Но, в силу чётности подынтегральной функции и симметрии её графика, достаточно вычислить площадь синей фигуры, а результат удвоить. Одинаковые же половинки! численно равен площади фигуры, которая заштрихована серым цветом. Но, в силу чётности подынтегральной функции и симметрии её графика, достаточно вычислить площадь синей фигуры, а результат удвоить. Одинаковые же половинки!
Возможно, некоторые скажут: «Да зачем это всё нужно? – можно ведь и так вычислить определенный интеграл». Можно. Давайте вычислим:
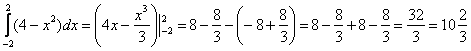
Но удобно ли было подставлять отрицательный нижний предел? Не очень-то. И «минус» тут частенько теряют. Поэтому гораздо проще и приятнее подставить ноль.
Замечу также, что это ещё был простой демонстрационный пример, на практике всё бывает хуже, особенно, когда имеешь дело с двойными и тройными интегралами, где вычислений и так хватает.
Разминочный интеграл для самостоятельного решения:
Пример 22
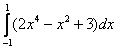
И обратите внимание, что когда вам предложено ПРОСТО ВЫЧИСЛИТЬ определенный интеграл, то чертеж выполнять не нужно! Достаточно убедиться в чётности функции (как правило, устно) и перед решением сделать соответствующий письменный комментарий. Кстати, о птичках:
Пример 23
1) Вычислить определенный интеграл: 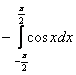 . .
2) Вычислить площадь плоской фигуры, ограниченной линией 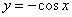 и осью и осью 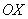 на промежутке на промежутке 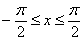 . .
Внимание! Это две РАЗНЫЕ задачи! Решаем:
1) Подынтегральная функция является чётной, отрезок интегрирования симметричен относительно нуля, поэтому:
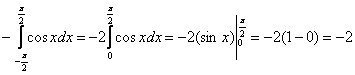 – определённый интеграл получился отрицательным, и так бывает! – определённый интеграл получился отрицательным, и так бывает!
2) Теперь задача на нахождение площади фигуры:
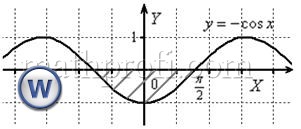
На отрезке 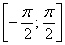 график функции расположен ниже оси график функции расположен ниже оси 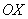 , поэтому: , поэтому:
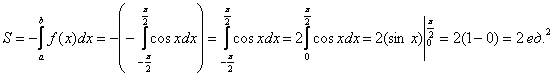 – площадь отрицательной быть не может! Знак «минус» в формуле и не позволил. – площадь отрицательной быть не может! Знак «минус» в формуле и не позволил.
Заметьте, что чётность косинуса никто не отменял, поэтому мы опять споловинили отрезок и удвоили интеграл.
Творческий пример для самостоятельного решения + новинка:
Пример 24
Вычислить площадь круга, ограниченного окружностью 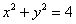
Напоминаю, что уравнение 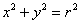 задаёт окружность радиуса задаёт окружность радиуса 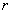 с центром в начале координат; а функции с центром в начале координат; а функции 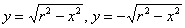 – верхнюю и нижнюю полуокружности соответственно. – верхнюю и нижнюю полуокружности соответственно.
Новизна же состоит в ранее не встречавшейся замене 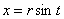 , где новые пределы интегрирования удобно отыскать из обратной функции , где новые пределы интегрирования удобно отыскать из обратной функции 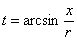 . И, конечно, приятно, что ответ известен заранее, по школьной формуле, площадь круга: . И, конечно, приятно, что ответ известен заранее, по школьной формуле, площадь круга:
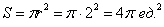
Забавно, что формула и выводится с помощью этого интеграла.
 1.11. А если подынтегральная функция нечётная? 1.11. А если подынтегральная функция нечётная?
 1.9. Объём тела вращения 1.9. Объём тела вращения
| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
|